Skip to main content

Trees

Tree Core Algorithms

In trees, there are two main points of view: recursive and iterative.

Core algorithms include (1) BST methods, (2) PreOrderRecursive, (3) PreOrderIterative, (4) InOrderRecursive, (5) InOrderIterative, (6) PostOrder recursive, (7) PostOrderIterative, (8) BFS, (9) DFS, (10) LevelOrder. Once you completely understand these, you can solve any tree question.

private static class Node {
  Node left;
  Node right;
  int value;
  
  public Node(Node left, Node right, int value) {
    this.left = left;
    this.right = right;
    this.value = value;
  }
  
  public Node(int value) {
    this.left = null;
    this.right = null;
    this.value = value;
  }
}

BST Methods​

The followings are the BST insert, search, delete, and clone functions.

  1. BST insert function
  • I was wondering how is there always a space for a data to be inserted in a binary search tree? That's because the inputs are discrete numbers so there's always a space. For example, an example of a dense tree is a balanced tree with these nodes: 1,2,3. The only nodes you can insert now are number less than 2 or greater than 4. Assume an input value is 1 and there's a space for it. Same goes for 5. Now imagine inserting 5, 6, and 7 sequentially. It will create a linked list with the values and there's space for all of those numbers. 
public void insert(T data)
{
  root = insert(root, data);
}
private Node<T> insert(Node<T> p, T toInsert)
{
  if (p == null)
     return new Node<T>(toInsert);

  if (compare(toInsert, p.data) == 0)
    return p;

  if (compare(toInsert, p.data) < 0)
     p.left = insert(p.left, toInsert);
  else
     p.right = insert(p.right, toInsert);

  return p;
}
  1. BST search function
public boolean search(T toSearch)
{
  return search(root, toSearch);
}
private boolean search(Node<T> p, T toSearch)
{
  if (p == null)
     return false;
  else
  if (compare(toSearch, p.data) == 0)
    return true;
  else
  if (compare(toSearch, p.data) < 0)
     return search(p.left, toSearch);
  else
     return search(p.right, toSearch);
}
  1. BST delete function
public void delete(T toDelete)
{
  root = delete(root, toDelete);
}
private Node<T> delete(Node<T> p, T toDelete)
{
  if (p == null)  throw new RuntimeException("cannot delete.");
  else
  if (compare(toDelete, p.data) < 0)
    p.left = delete (p.left, toDelete);
  else if (compare(toDelete, p.data)  > 0)
    p.right = delete (p.right, toDelete);
  else
  {
     if (p.left == null) return p.right;
     else if (p.right == null) return p.left;
     else
     {
     // get data from the rightmost node in the left subtree
     // either rightmost from left subtree or leftmost from right subtree
        p.data = retrieveData(p.left);
     // delete the rightmost node in the left subtree
        p.left =  delete(p.left, p.data) ;
     }
  }
  return p;
}

private T retrieveData(Node<T> p)
{
  while (p.right != null) p = p.right;

  return p.data;
}
  1. BST clone function
public BST<T> clone()
{
 BST<T> twin = null;

 if(comparator == null)
    twin = new BST<T>();
 else
    twin = new BST<T>(comparator);

 twin.root = cloneHelper(root);
 return twin;
}
private Node<T> cloneHelper(Node<T> p)
{
 if(p == null)
    return null;
 else
    return new Node<T>(p.data, cloneHelper(p.left), cloneHelper(p.right));
}

// version2
private Node<T> cloneHelper(Node<T> p)
{
 if(p == null)
    return null;
 else
    Node copy = new Node<T>(p.data);
    copy.left = cloneHelper(p.left);
    copy.right = cloneHelper(p.right);
    return copy;
}

Preorder​

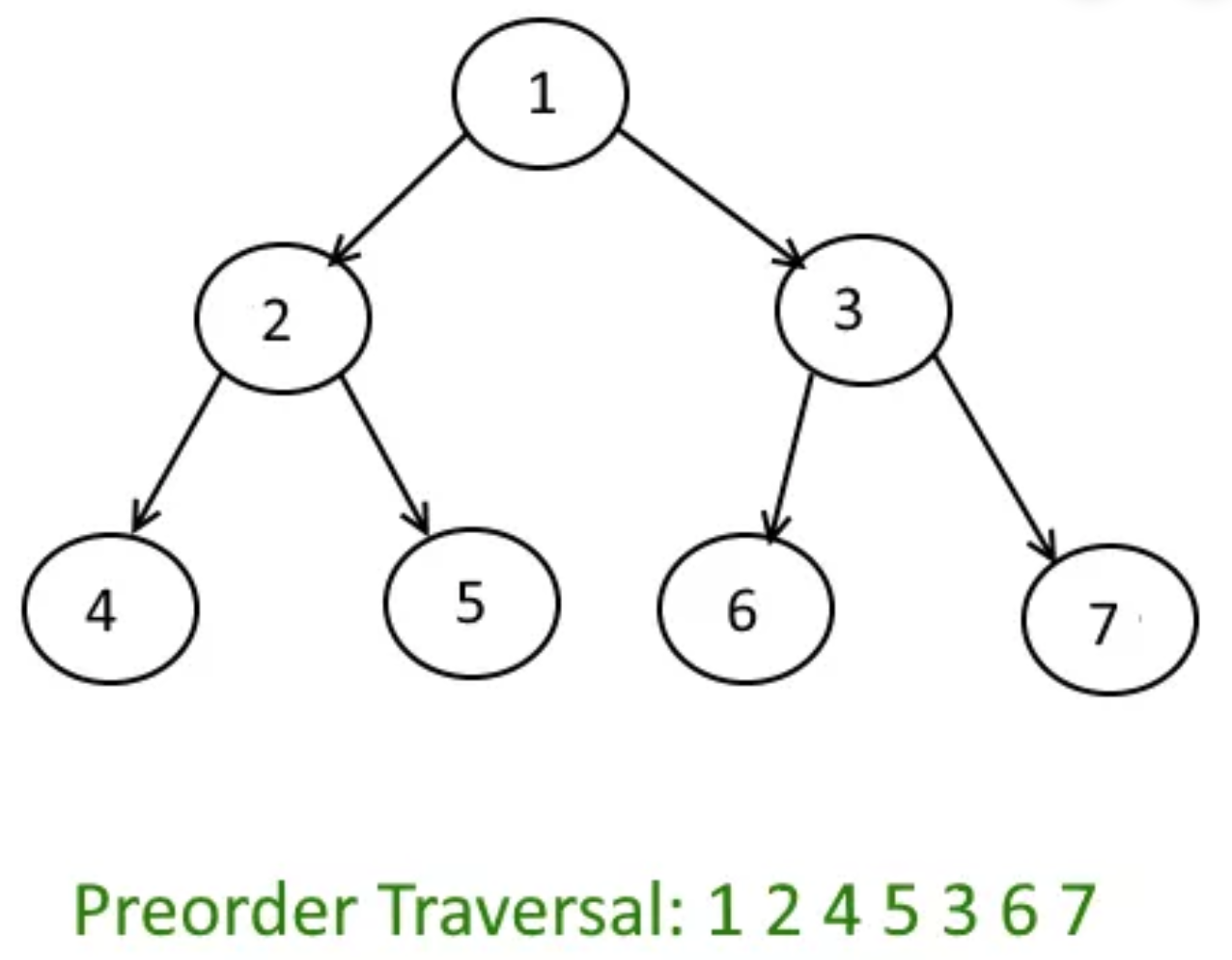
Locale Dropdown

Preorder Recursive​

public static void preorder(Node root) {
    if (root == null) {
        return;
    }
    System.out.println(root.data);
    preorder(root.left);
    preorder(root.right);
}

Preorder Iterative​

List<Integer> preorderIterative(TreeNode root) {

    List<Integer> list = new ArrayList<>();
    if (root == null) {
        return list;
    }
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);

    while (!stack.isEmpty()) {
        TreeNode popped = stack.pop();
        list.add(popped.val);

        // you want left to be printed first, so let's push right before left.
        if (popped.right != null) {
            stack.push(popped.right);
        }
        if (popped.left != null) {
            stack.push(popped.left);
        }
    }

    return list;
}

Inorder​

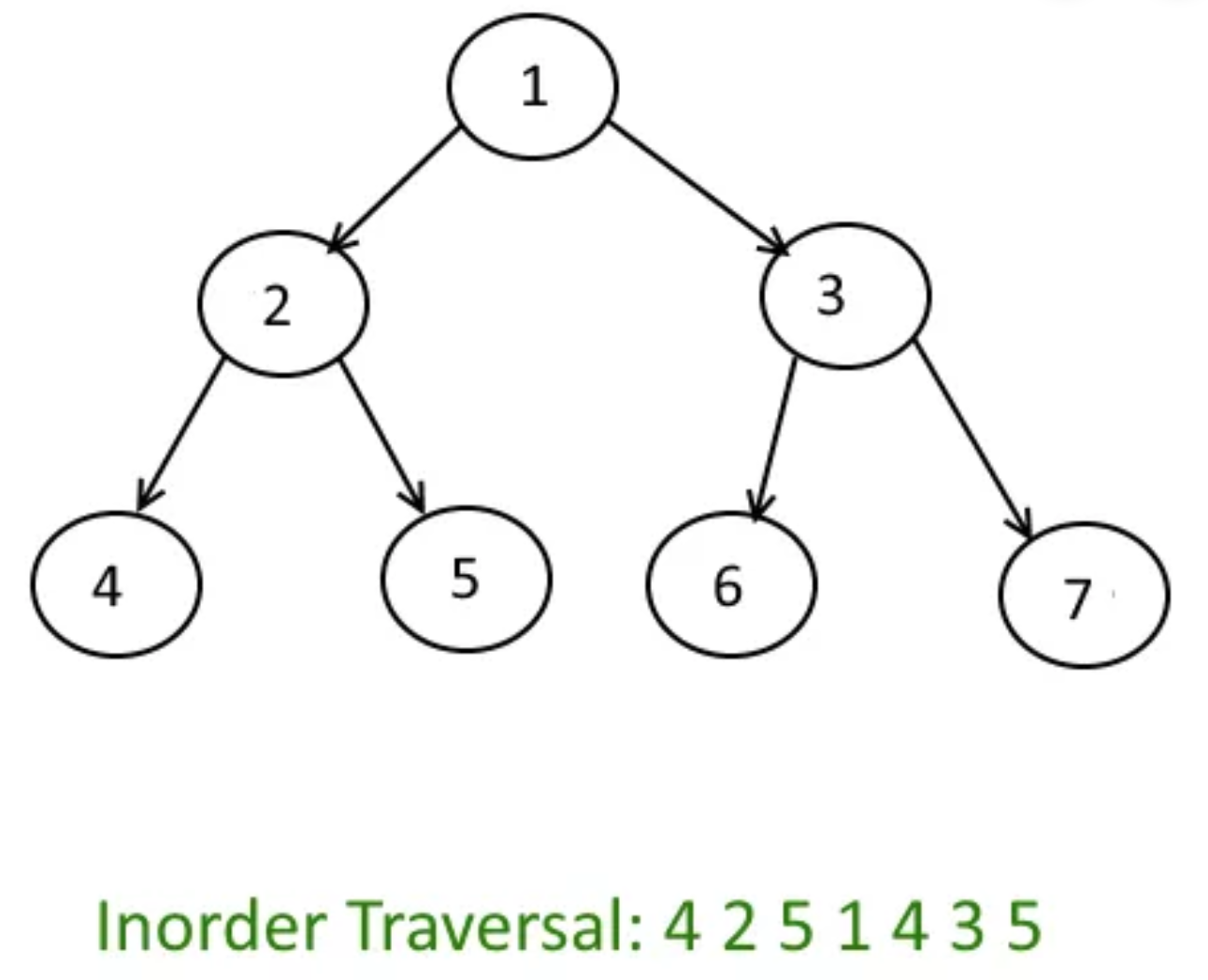
Inorder Traversal: 4 2 5 1 6 3 7 (The image has the order wrong) Locale Dropdown

Inorder Recursive​

public static void inorderRecur(Node root) {
    if (root == null) {
        return;
    }
    inorderRecur(root.left);
    System.out.println(root.data);
    inorderRecur(root.right);
}

Inorder Iterative​

public List<Integer> inorderTraversalIterative(TreeNode root) {
    List<Integer> result = new ArrayList<>();
    TreeNode cur = root;
    Stack<TreeNode> stack = new Stack<>();

    // TODO should it be AND or OR? - the explanation is written on step 4-b
    while (cur != null || !stack.isEmpty()) {
        while (cur != null) {
            stack.push(cur);
            cur = cur.left;
        }

        // cur is null at this point.
        TreeNode popped = stack.pop();

        result.add(popped.val);

        if (popped.right != null) {
            cur = popped.right;
        }

    }

    return result;}

Postorder​

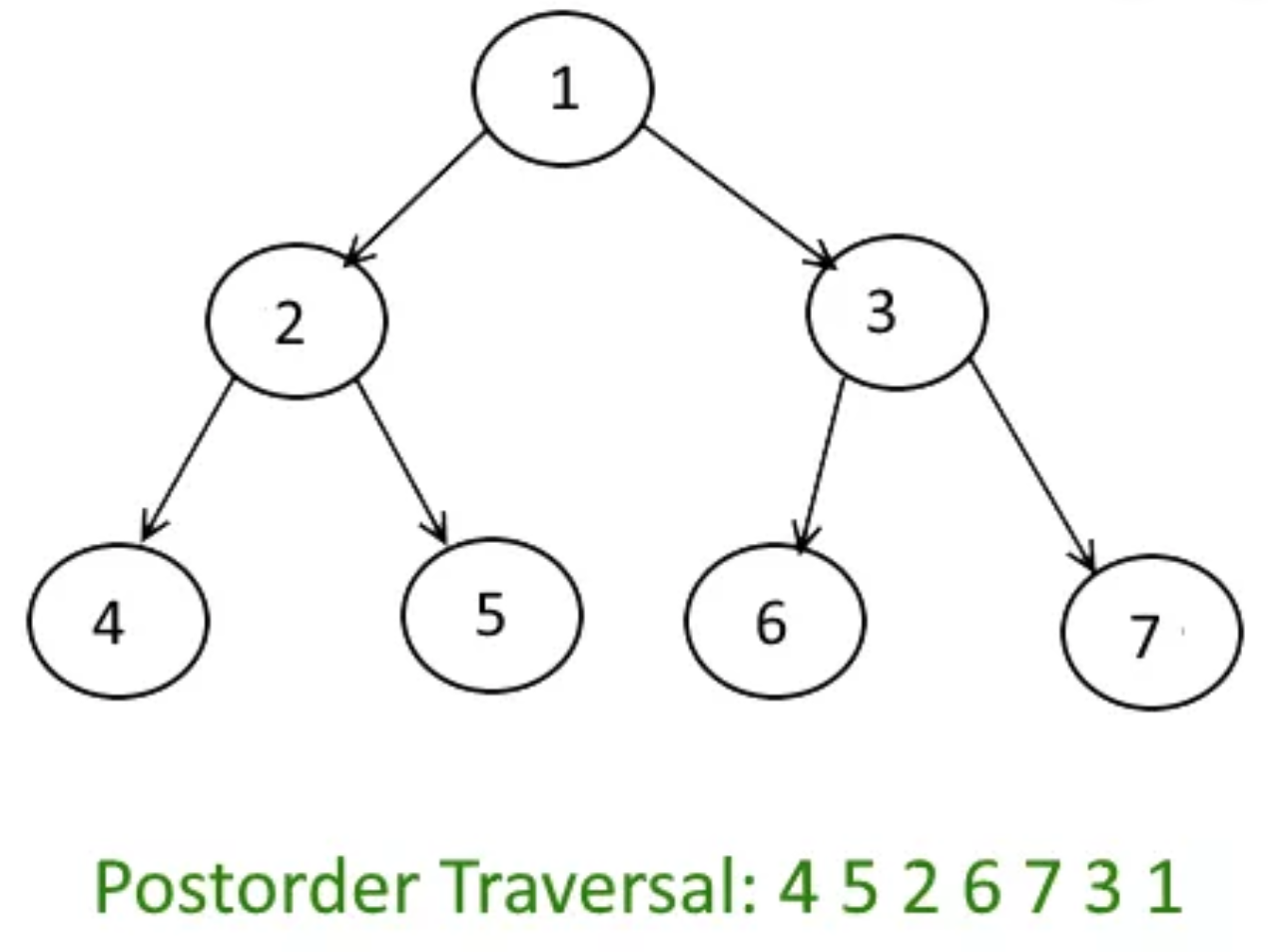
Locale Dropdown

Note that if you do postorder backwards, it's preorder except that its left and right are switched.

Postorder Recursive​

private void postOrder(Node root) {
    if (root == null) {
        return;
    }
    postOrder(root.left);
    postOrder(root.right);
    Utils.print(root.data);
}

Postorder Iterative​

public List<Integer> postorderTraversal(TreeNode root) {
    List<Integer> list = new ArrayList<>();
    if (root == null) {
        return list;
    }
    Stack<TreeNode> pre = new Stack<>();
    Stack<TreeNode> post = new Stack<>();

    pre.push(root);

    while (!pre.isEmpty()) {
        TreeNode popped = pre.pop();
        post.push(popped);

        if (popped.left != null) {
            pre.push(popped.left);
        }

        if (popped.right != null) {
            pre.push(popped.right);
        }
    }

    while (!post.isEmpty()) {
        TreeNode popped = post.pop();
        list.add(popped.val);
    }

    return list;
}

BFS​

Just replace PreOrder's Stack with a queue!

public static List<Integer> bfs(TreeNode root) {
    List<Integer> result = new ArrayList<>();

    if (root == null) {
        return result;
    }

    Queue<TreeNode> queue = new LinkedList<>();
    while (!queue.isEmpty()) {
        TreeNode popped = queue.poll();
        result.add(popped.val);
        if (root.left != null) {
            queue.add(root.left);
        }

        if (root.right != null) {
            queue.add(root.right);
        }
    }

    return result;

DFS​

Its algorithm is same as that of preorder

Level Order​

    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> ans = new ArrayList<>();
        if (root == null) return ans;
        
        queue.add(root);
        while (!queue.isEmpty()) {
            int queueSize = queue.size();
            List<Integer> levelList = new ArrayList<>();
            for (int i = 0; i < queueSize; i++) {
                TreeNode popped = queue.poll();
                levelList.add(popped.val);
                if (popped.left != null) {
                    queue.add(popped.left);
                }
                if (popped.right != null) {
                    queue.add(popped.right);
                }
            }
            ans.add(levelList);
        }
        
        return ans;
    }

levelorder

Question2: What is the difference between BFS and Level order?​

BFS doesn't have to divide between levels, you cannot tell from the final output how many levels there are in the tree, hence the use of queue; LevelOrder has division between each level and we cannot merge all nodes together in a list.