Sorting
Algorithms to go over:
- Quick sort algorithm
private int partition (int[] arr, int start, int end) {
int pivot = arr[end];
// low is the trailing end of the section with numbers lower than the pivot.
int low = start - 1;
for (int cur = start; cur <= end - 1; cur++) {
if (arr[cur] < pivot) {
low++;
swap(arr, low, cur);
}
}
// Make sure to swap the index not pivot value
swap(arr, low + 1, end);
return low + 1;
}
public void quickSort (int[] nums, int start, int end) {
if (end < start) return;
int pi = partition(nums, start, end);
quickSort(nums, start, pi - 1);
quickSort(nums, pi + 1, end);
}
- Quick Select algorithm
- Time complexity: O(n), with a worst-case of O(n^2).
public int kthSmallest(int[] nums, int start, int end, int k) {
int p = partition(nums, start, end);
if (pivot == k) {
return nums[p];
} else if (k < p) {
return kthSmallest(nums, start, p - 1, k);
} else { // k > p
return kthSmallest(nums, p + 1, end, k);
}
}
- Insertion sort
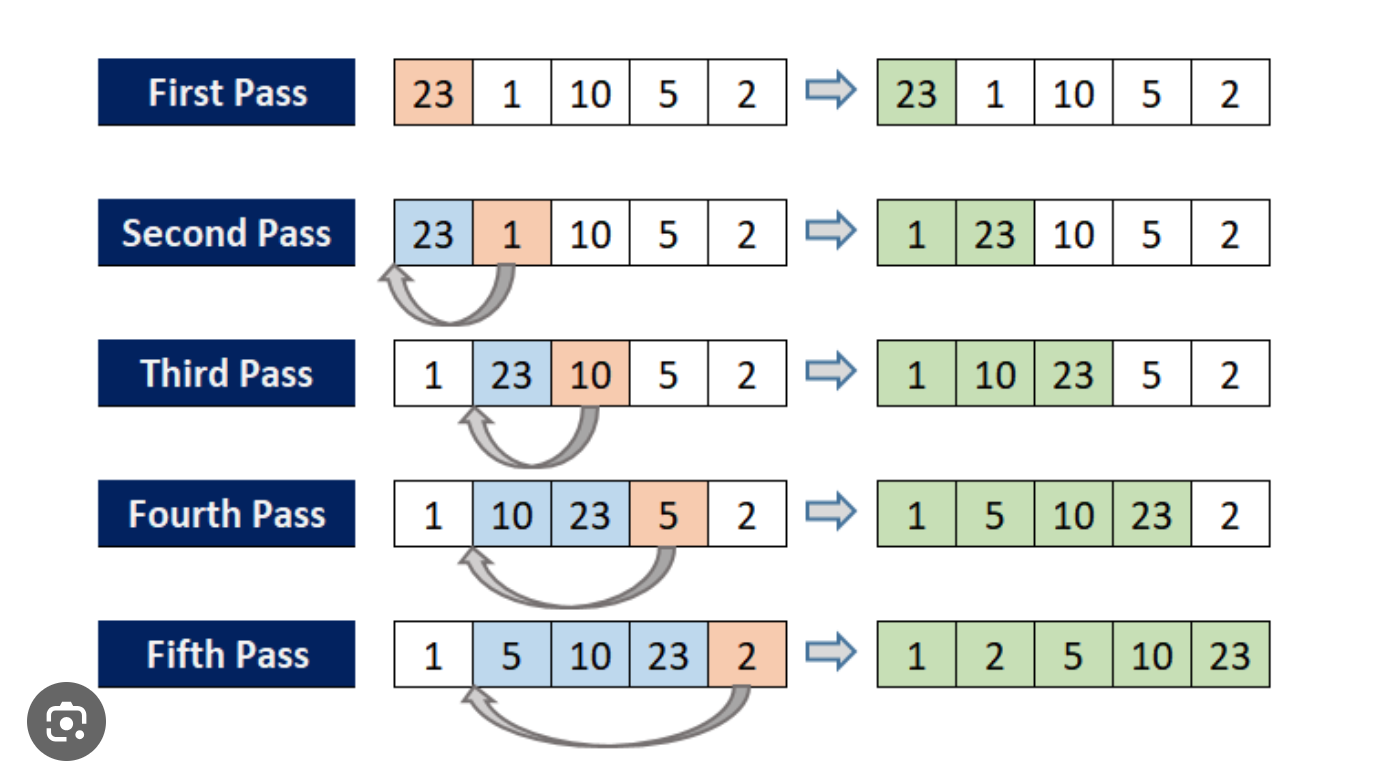
public static void insertionSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
int key = nums[i];
int j = i - 1;
while (0 <= j && key < nums[j]) {
// swap
nums[j + 1] = nums[j];
j--;
}
nums[j + 1] = key;
}
}
- How to use the comparator
Comparator
- It is an interface.
How to use it? One example is using it as an anonymous class.
Since Comparator is an interface, by calling new Interface, you are creating an anonymous class.
if (A < B) { // (1, 5) is compared
return -1;
} else if (B > A) { // (5, 1) is compared
return 1;
} else { // (3, 3) is compared
return 0;
}
In compare, if you want to make it an ascending order, left < right is -1. left > right is +1.
If you want to make it a descending order, left < right is +1 and right > left is -1.
public List<Integer> sortTupleArray(Integer[][] array) {
Arrays.sort(array, new Comparator<Integer[]>() {
@Override
public int compare(Integer[] left, Integer[] right) {
if (left[0] < right[0]) {
return -1;
} else if (left[0] > right[0]) {
return 1;
} else {
return 0;
}
}
});
}
The above code is equivalent to
public List<Integer> sortTupleArray(Integer[][] array) {
Arrays.sort(array, new Comparator<Integer[]>() {
@Override
public int compare(Integer[] left, Integer[] right) {
return (left[0] - right[0]);
}
});
}
To make it even shorter, you can use lambda
public List<Integer> sortTupleArray(Integer[][] array) {
Arrays.sort(array,
(int[] left, int[] right) -> (left[0] - right[0])
);
}
To add an if statement in lambda
public List<Integer> sortTupleArray(Integer[][] array) {
Arrays.sort(array,
(int[] left, int[] right) -> {
if (left[0] < right[0]) {
return -1;
} else if (left[0] > right[0]) {
return +1;
} else {
return 0;
}
}
);
}
Practice Problems
Quick Select problems
- https://leetcode.com/problems/kth-largest-element-in-an-array/
- https://leetcode.com/problems/k-closest-points-to-origin/
- https://leetcode.com/problems/top-k-frequent-words/
- The following move zeroes problem can use quicksort's partition function. It gives you a different insight of the partition function.
- One insight is that the values that are moved to the left will maintain its order but the values on the right cannot maintain its order. Here the order being the index order corresponding to the values.
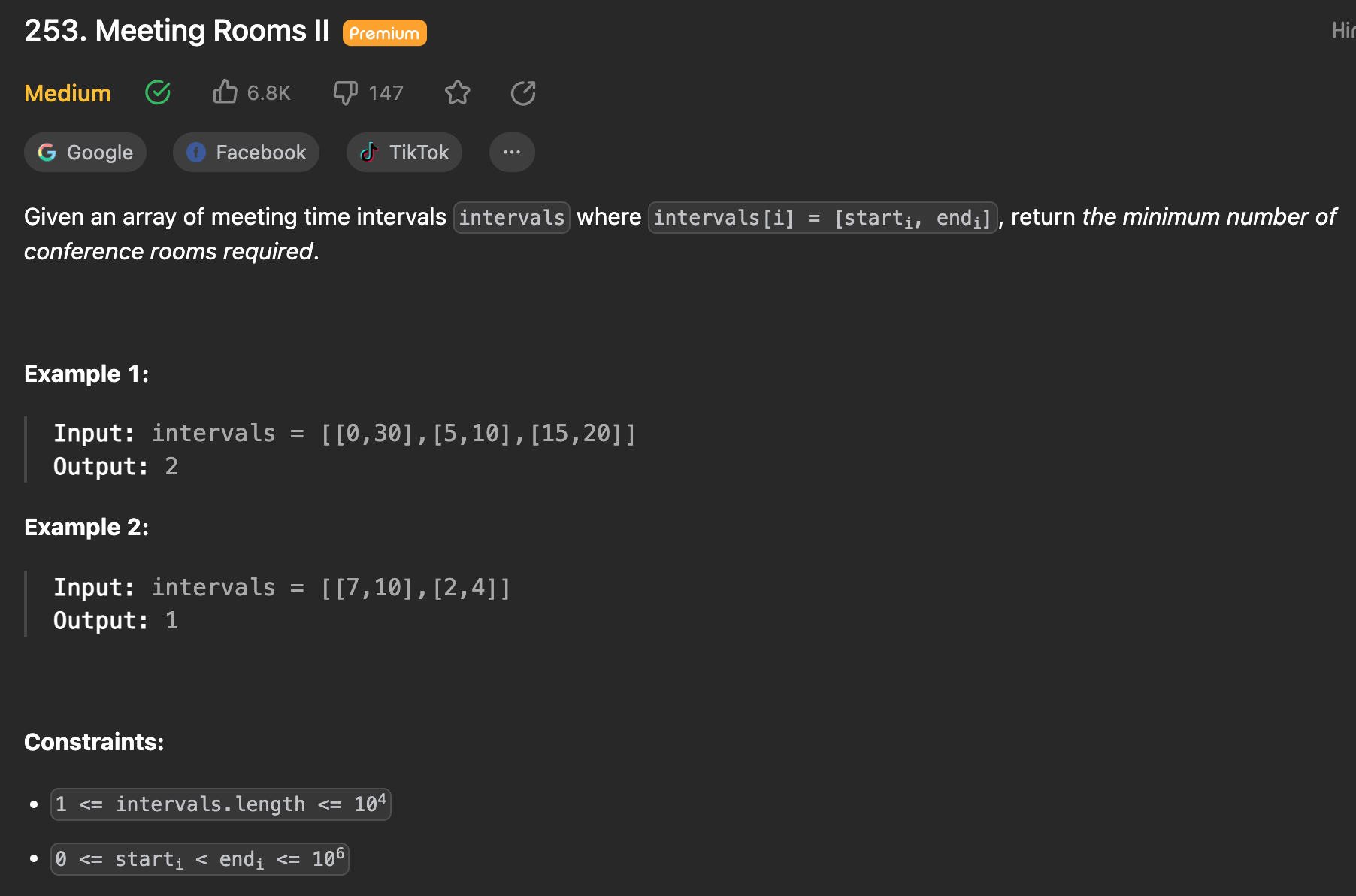
Meeting Room Problems
public int[][] merge(int[][] intervals) {
List<int[]> result = new ArrayList<>();
Arrays.sort(intervals, (left, right) -> left[0] - right[0]); // NlogN
result.add(intervals[0]);
for (int i = 1; i < intervals.length; i++) {
int[] cur = intervals[i]; // [7,8]
int[] prev = result.get(result.size() - 1);
if (prev[1] >= cur[0]) {
result.remove(result.size() - 1);
int[] newItem = new int[2]; // [0,6]
newItem[0] = Math.min(prev[0], cur[0]);
newItem[1] = Math.max(prev[1], cur[1]);
result.add(newItem);
} else {
result.add(cur);
}
}
return result.toArray(new int[result.size()][]);
//return convertToArray(result);
}
public boolean canAttendMeetings(int[][] intervals) {
TreeSet<int[]> set = new TreeSet<>((int[] left, int[] right) -> {
if (left[1] <= right[0] && left[1] < right[1]) {
return -1;
} else if (left[0] >= right[1] && left[1] > right[1]) {
return +1;
} else {
return 0;
}
});
for (int[] interval : intervals) {
if (set.contains(interval)) {
return false;
}
set.add(interval);
}
return true;
}
Another treeset is
/**
| |
[1, 2] [3, 4]
| |
[3, 4] [1, 2]
*/
TreeSet<int[]> set = new TreeSet<>((a, b) -> {
if (a[1] <= b[0]) {
return -1;
} else if (b[1] <= a[0]) {
return 1;
} else {
return 0;
}
});
Edge cases to think about
- [[0,30],[5,10],[15,20]]
- [[7,10],[2,4]]
- [[9,10],[4,9],[4,17]]
- [[1,5],[8,9],[8,9]]
public int minMeetingRooms(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> (a[0] - b[0]));
PriorityQueue<int[]> endQueue = new PriorityQueue<>((a, b) -> (a[1] - b[1]));
for (int[] interval : intervals) { //[1, 5], [8,9]
//System.out.println(interval[0]);
if (!endQueue.isEmpty()) {
int prevEndTime = endQueue.peek()[1]; // don't poll
int curStartTime = interval[0]; // important
if (curStartTime < prevEndTime) { // important
} else {
endQueue.poll();
}
}
endQueue.add(interval);
}
return endQueue.size();
}
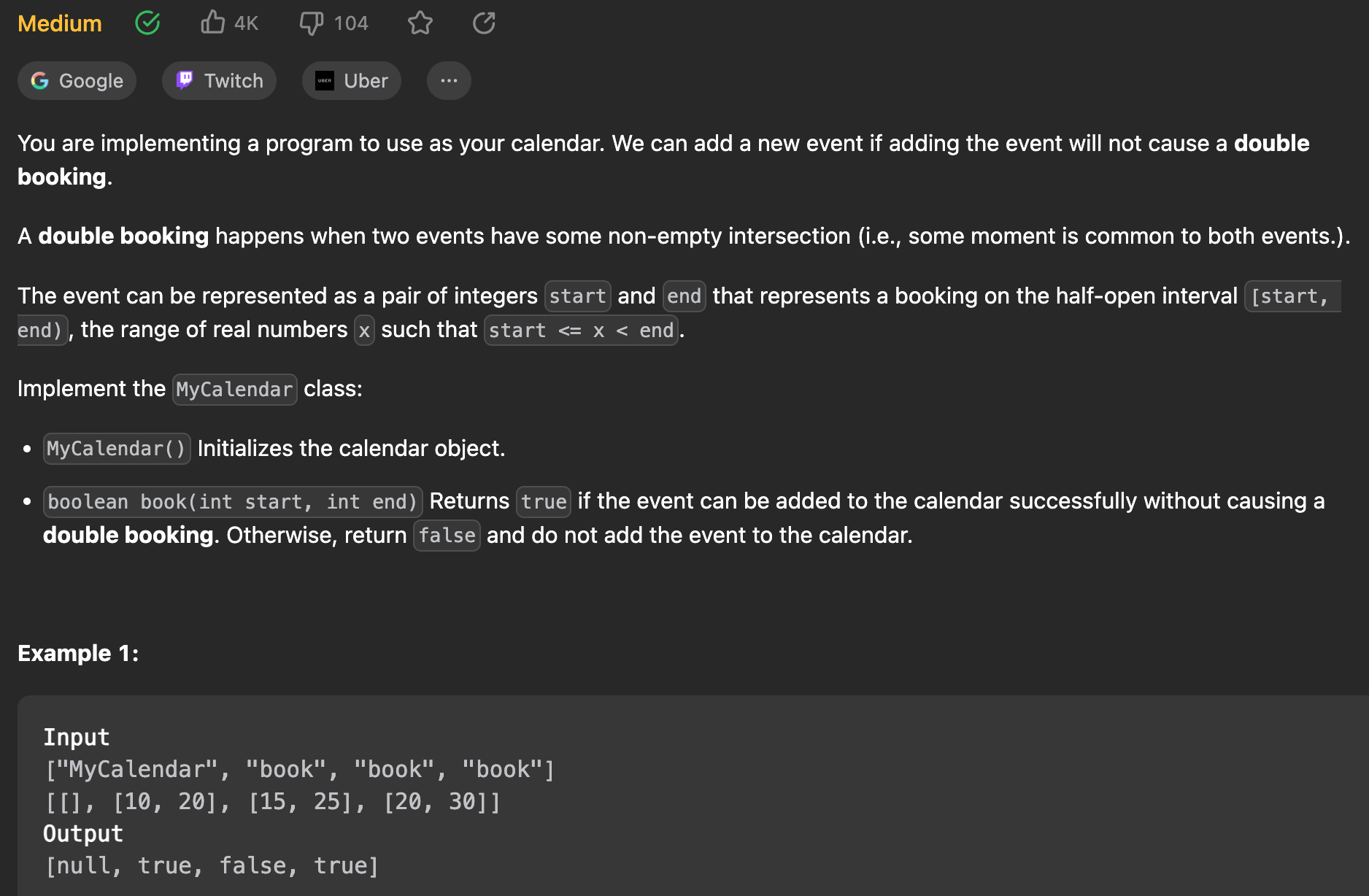
- Brute force is N^2 and optimize with treeset
class MyCalendar {
TreeSet<int[]> set;
public MyCalendar() {
set = new TreeSet<>((left, right) -> {
if (left[1] <= right[0]) return -1;
else if (left[0] >= right[1]) return +1;
else return 0;
});
}
public boolean book(int start, int end) {
int[] curItem = new int[] {start, end};
if (set.contains(curItem)) return false;
set.add(curItem);
return true;
}
}
- https://leetcode.com/problems/my-calendar-ii/description/
- https://leetcode.com/problems/my-calendar-iii/description/
- https://leetcode.com/problems/car-pooling/