Backtracking

Permutation	Combination
Order matters	Order does't matter
lock	fruit salad

Permutation

• Order matters
• For permuation, loop should start from i = 0.

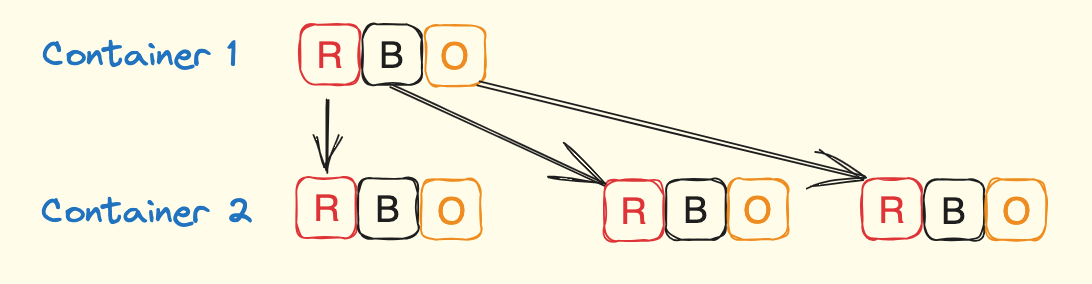
Permutation with repetition

• N^R different possibilities
• e.g. Given red, blue, orange, how many permutations are there to fill up 2 containers? 3^2

private List<List<Integer>> result;
private List<Integer> intermList;
public List<List<Integer>> permutationWithRepetition(int[] colors) {
  result = new ArrayList<>();
  intermList = new ArrayList<>();
  permutationWithRepetition(colors, 2, 0);
  permutationWithRepetition2(colors, 2);
}   
private void permutationWithRepetition(int[] colors, int containerDepth, int depth) {
  if (depth == containerDepth) {
      result.add(new ARrayList<>(intermList));
      return;
  }
  for (int i = 0; i < colors.length; i++) {
    intermList.add(colors[i]);
    permutationWithRepetition(colors, depth + 1);
    intermList.remove(intermList.size());
  }
}
private void permutationWithRepetition2(int[] colors, int containerDepth) {
    for (int i = 0; i < colors.length; i++) {
        intermList.add(colors[i]);
        if (intermList.size() == containerDepth) {
            result.add(new ARrayList<>(intermList));
            intermList.remove(intermList.size());
            conitnue;
        }
        permutationWithRepetition2(colors, containerDepth);
        intermList.remove(intermList.size());
    }
}

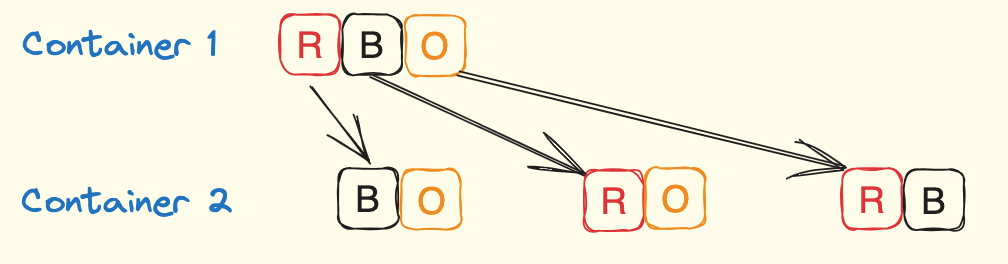
Permutation without repetition

• N!/(N-R)!
• Given red, blue, orange, how many permutations are there to fill up 2 containers without using one color more than once?

The following problem is from Leetcode - 46. Permutations Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

Input: nums = [1,2,3]

Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

• Time complexity: O(N * N!)?
• Space complexity: O(N!)

Would the following code work?

private void permute(int[] nums, int curI) {
  if (set.size() == nums.length) {
    result.add(new ArrayList<>(set));
    return;
  }
  if (curI == nums.length) return;

  for (int i = 0; i < nums.length; i++) {
    int curVal = nums[curI];
    if (!set.contains(curVal)) {
      set.add(curVal);
      permute(nums, curI + 1);
      set.remove(curVal);
    }
  }
}

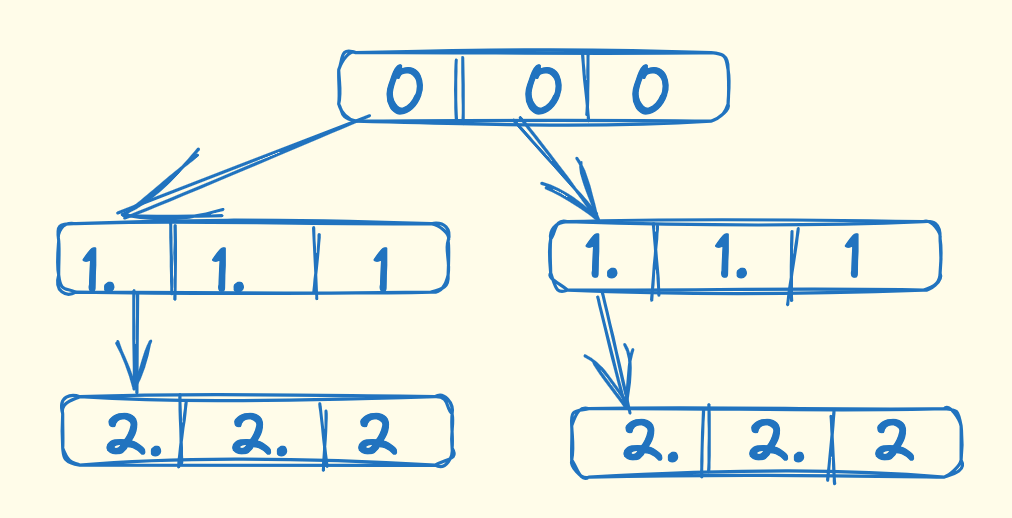
It doesn't work, because the set does not store chronological order unlike list. Also, there's a major bug here about the way tree is created. The following fixes the tree structure, but the set is still there.

private static void permute(int[] nums, int curI, Set<Integer> set,
                                List<List<Integer>> result) {
    if (set.size() == nums.length) {
        result.add(new ArrayList<>(set));
        Util.print(result);
        return;
    }

    for (int i = 0; i < nums.length; i++) {
        int curVal = nums[i];
        if (!set.contains(curVal)) {
            set.add(curVal);
            permute(nums, curI + 1, set, result);
            set.remove(curVal);
        }
    }
}

How about this one?

public List<List<Integer>> permute(int[] nums) {
    interm = new ArrayList<>();
    result = new ArrayList<>();
    permute(nums, new boolean[nums.length], 0);
    return result;
}
private List<Integer> interm;
private List<List<Integer>> result;
private void permute(int[] nums, boolean[] seen, int depth) {

    if (depth == nums.length) {
        result.add(new ArrayList<>(interm));
        return;
    }
    for (int i = 0; i < nums.length; i++) {
        if (seen[i] == false) {
            seen[i] = true;
            interm.add(nums[i]);
            permute(nums, seen, depth + 1);
            interm.remove(interm.size() - 1);
            seen[i] = false;
        }
    }
}

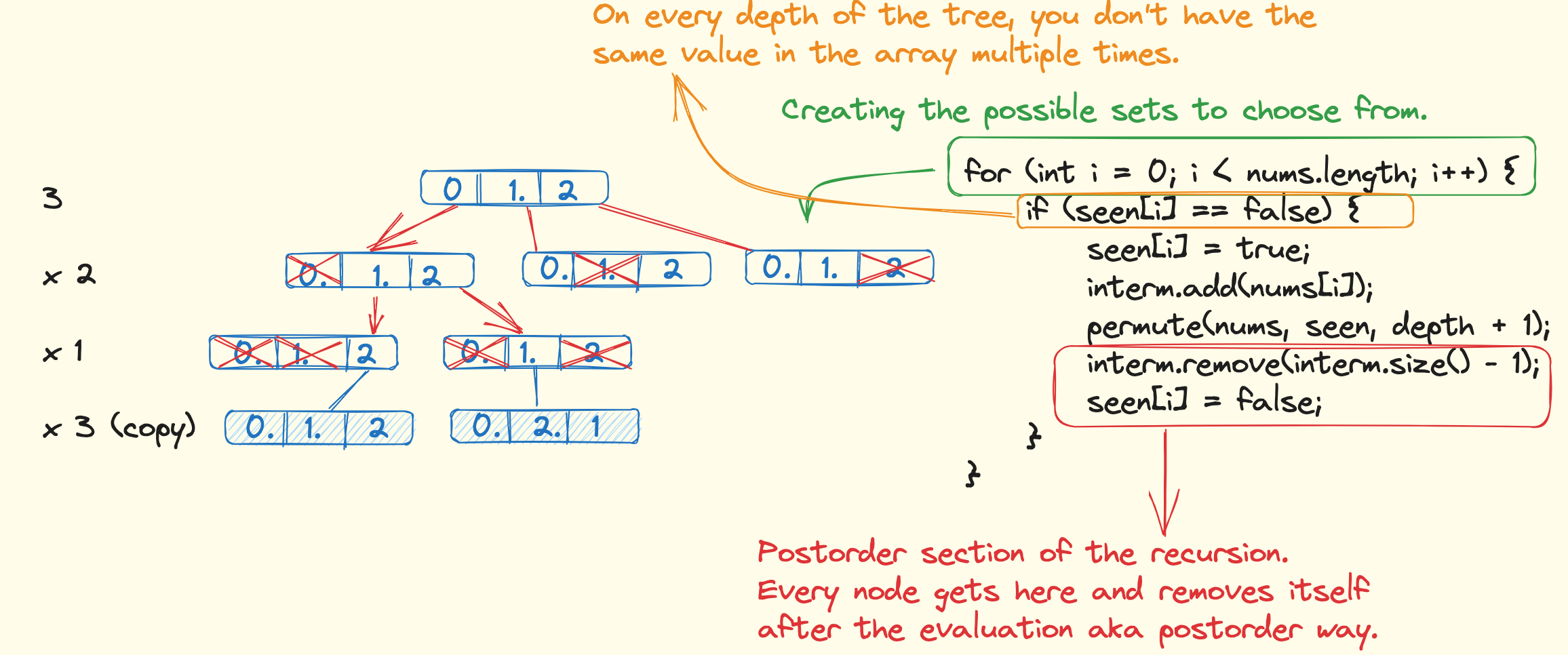
This one works because it's the right tree like below. The time complexity is n! from the recursive calls and n is multiplied on every end of the n! branch to copy the result.

How about this one

private void permute(int[] nums, List<Integer> interm, List<List<Integer>> result, boolean[] visited) {
    
    for (int cur = 0; cur < nums.length; cur++) {//cur =2
      if (visited[cur] == true) continue;
      interm.add(nums[cur]); // 3
      visited[cur] = true; // 
      if (interm.size() == visited.length) {
        result.add(new ArrayList<>(interm));
        visited[cur] = false;
        interm.remove(interm.size() - 1);
        return;
      }
      permute(nums, interm, result, visited);
      interm.remove(interm.size() - 1);
      visited[cur] = false;
    }
}

This one works too. This one short circuits without going one more level deeper to stop the recursion.

• Time complexity: O(N * N!)
• Space complexity: O(N N!) = O(N) for the recursion stack depth and O(N!N) for the result.

Permutation with duplicate values in the set

• N!/(R1!*R2!) where R1 and R2 are duplicate values.
• Given ABBCC, how many permutations are there to rearrange ABBCC? 5!/(2! 2!)
• Identical to the permutation code except saving the result in the set instead.

public List<List<Integer>> permuteUnique(int[] nums) {
    Set<List<Integer>> set = new HashSet<>();
    perm(nums, new ArrayList<>(), set, new boolean[nums.length], 0);
    return new ArrayList<>(set);
}
private void perm(int[] nums, List<Integer> interm, Set<List<Integer>> result, boolean[] visited, int level) {
    if (level == nums.length) {
        result.add(new ArrayList<>(interm));
        return;
    }
    for (int i = 0; i < nums.length; i++) {
        if (visited[i] == true) continue;
        visited[i] = true;
        interm.add(nums[i]);
        perm(nums, interm, result, visited, level + 1);
        interm.remove(interm.size() - 1);
        visited[i] = false;
    }   
}
* Time complexity: O(N * N!) assuming the case where there's no duplciate. With duplicate it would be something like N!/(R1!*R2!) where R1 and R2 are duplicate values and you have to multply N to the whole thing to copy the result. 
* Space complexity: O(N * N!) = O(N) for the recursion stack depth and O(N!*N) for the result.

Combination

• Order doesn't matter like fruit salad

Combination without repetition

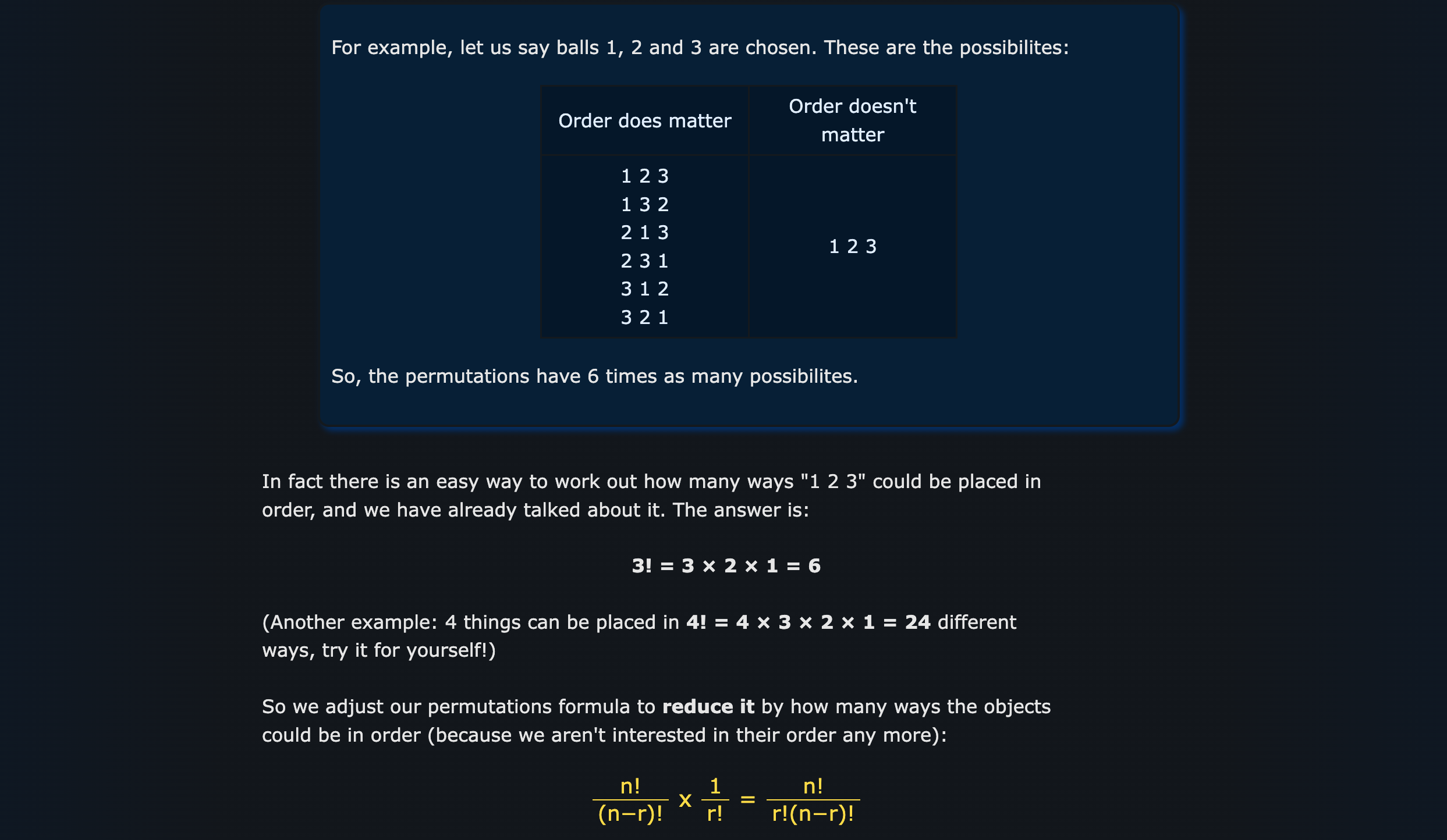
• N!/((N-R)! R!)
• The following problem is from Leetcode - 77. Combinations
• Time complexity: O( n!/(k!*(n-k)!) )
• Space complexity: O(k)

Combination Preorder and Postorder

  public List<List<Integer>> combine(int n, int k) {
    List<List<Integer>> result = new ArrayList<>();
    //combinePreorder(n, 1, k, new ArrayList<>(), result);
    //return result;
    return combinePostorder(n, 1, 0, k);
  }
  // TODO: Change the return list to linkedlist from arraylist to reduce time complexity when adding to the front.
  private List<List<Integer>> combinePostorder(int n, int start, int depth, int depthLimit) {
    if (depth == depthLimit) {
      // very important
      return new ArrayList<>() {{add(new ArrayList<>());}};
    }

    List<List<Integer>> siblingWork = new ArrayList<>();
    for (int i = start; i <= n; i++) {
      List<List<Integer>> childWork = combinePostorder(n, i + 1, depth + 1, depthLimit);
      for (List<Integer> childWorkVal : childWork) {
        childWorkVal.add(0, i);
        siblingWork.add(childWorkVal);
      }
    }
    return siblingWork;
  }

  private void combinePreorder(int n, int start, int depthLimit, List<Integer> interm, List<List<Integer>> result) {
    if (interm.size() == depthLimit) {
      result.add(new ArrayList<>(interm));
      return;
    }
    for (int i = start; i <= n; i++) {
      interm.add(i);
      combinePreorder(n, i + 1, depthLimit, interm, result);
      interm.remove(interm.size() - 1);
    }
  }

preorder

public List<List<Integer>> combine(int n, int k) {
    Set<List<Integer>> ans = new HashSet<>();
    if (k > n) {
        return new ArrayList<>(ans);
    }
    preorder(n, k, ans, new ArrayList<>());
    return new ArrayList<>(ans);
}

private void preorder(int start, int k, Set<List<Integer>> ans, List<Integer> interm) {
    if (k == 0) {
        ans.add(new ArrayList<>(interm));
        return;
    }
    while (start != 0) { // 3
        interm.add(start);
        preorder(start - 1, k - 1, ans, interm);
        interm.remove(interm.size() - 1);
        start--;
    }
}

postorder

private List<List<Integer>> postorder(int start, int k) {
    // if (start < 0) {
    //     return new ArrayList<>();
    // }
    if (k == 0) {
        return new ArrayList<>(){{add(new ArrayList<>());}};
    }
    
    List<List<Integer>> siblingWork = new ArrayList<>();
    while (start != 0) {
        List<List<Integer>> childWork = postorder(start - 1, k - 1);
        for (List<Integer> list : childWork) {
            list.add(start);
            siblingWork.add(list);
        }
        start--;
    }
    return siblingWork;
}

Combination with repetition

• (R + N - 1)! / (R! (N - 1)!)
• The following problem is from Leetcode - Combination Sum
• Time complexity: O(N*2^N)
• Space Complexity: O(N*k) where k is the average size of the answer

Preorder

public List<List<Integer>> combinationSum(int[] candidates, int target) {
    Set<List<Integer>> ans = new HashSet<>();
    preorder(candidates, 0, target, ans, new ArrayList<>());
    return new ArrayList<>(ans);
}

private void preorder(int[] candidates, int level, int target, Set<List<Integer>> ans, List<Integer> interm) {
    
    if (level == candidates.length) return;
    
    int repeat = 0;
    int total = 0;
    
    int cur = candidates[level];
    while (total <= target) {
        
        if (repeat != 0) {
            interm.add(cur);
        }
        if (total == target) {
            ans.add(new ArrayList<>(interm));
        }
        
        preorder(candidates, level + 1, target - total, ans, interm);
        
        repeat++;
        total = repeat * cur;
    }
    // removing siblings from interm
    while(--repeat != 0) {interm.remove(interm.size() - 1);}
}

• https://leetcode.com/problems/letter-combinations-of-a-phone-number/

• Time complexity: O(4^N)

• Space complexity: O(4^N * N)

preorder

private String digits;
private Map<Character, String> map;
public List<String> letterCombinations(String digits) {
    this.digits = digits;
    this.map = new HashMap<>();
    map.put('2', "abc");
    map.put('3', "def");
    map.put('4', "ghi");
    map.put('5', "jkl");
    map.put('6', "mno");
    map.put('7', "pqrs");
    map.put('8', "tuv");
    map.put('9', "wxyz");
    List<String> ans = new ArrayList<>();
    if (digits.length() == 0) return ans;
    function(0, 0, ans, new StringBuilder());
    return ans;
}

private void function(int istart, int order, List<String> ans, StringBuilder sb) {
    if (order == digits.length()) {
        ans.add(sb.toString());
        return;
    }
    
    char bundle = digits.charAt(order);
    String comb = map.get(bundle);
    for (int i = istart; i < comb.length(); i++) {
        sb.append(comb.charAt(i));
        function(0, order + 1, ans, sb);
        sb.deleteCharAt(sb.length() - 1);
    }
}

postorder

private List<String> function(int order) {
    if (order == digits.length()) {
        return new ArrayList<>();
    }
    
    char bundle = digits.charAt(order);
    String comb = map.get(bundle);
    List<String> myWork = new ArrayList<>(); // used by every sibling
    
    for (int i = 0; i < comb.length(); i++) {
        List<String> childWork = function(order + 1);
        
        if (childWork.size() == 0) {
            myWork.add(comb.substring(i, i + 1));
        } else {
            for (String s : childWork) {
                myWork.add(comb.substring(i, i + 1) + s);
            }
        }
    }
    return myWork;
}

• https://leetcode.com/problems/subsets-ii/
• Time Complexity: O(2^N)
• Space Complexity: O(2^N * N)

preorder

public List<List<Integer>> subsetsWithDup(int[] nums) {
    Set<List<Integer>> ans = new HashSet<>();
    Arrays.sort(nums);
    preorder(nums, 0, ans, new ArrayList<>());
    return new ArrayList<>(ans);
}

private void preorder(int[] nums, int start, Set<List<Integer>> answer, List<Integer> interm) {
    answer.add(new ArrayList<>(interm));
    if (start == nums.length) {
        return;
    }
    
    for (int i = start; i < nums.length; i++) {
        interm.add(nums[i]);
        preorder(nums, i + 1, answer, interm);
        interm.remove(interm.size() - 1); // remove the current node before moving on to the next sibling
    }
}

postorder

private Set<List<Integer>> postorder(int[] nums, int start) {
    if (start == nums.length) {
        Set<List<Integer>> ans = new HashSet<>() {{
            add(new ArrayList<>());
        }};
        return ans;
    }
    
    Set<List<Integer>> childWork = postorder(nums, start + 1);
    Set<List<Integer>> curWork = new HashSet<>();
    for (List<Integer> list : childWork) {
        curWork.add(list);
        List<Integer> newList = new ArrayList<>(list);
        newList.add(nums[start]); // important - the order of which one you add first matters in set
        curWork.add(newList);
    }
    return curWork;
}

• https://leetcode.com/problems/palindrome-partitioning/
• https://leetcode.com/problems/generate-parentheses/