Recursion Practice
Induction Proof
I recommend that you take a look at an induction proof. It gives you an idea how to solve tree problems in a recursive way. There are three types of nodes you need to think about: 1. Base case (often times null node or leaf node), 2. An in-between node 3. Root node. From now on, I will call those nodes Main Nodes.
Different types of Recursive Functions
I categorize recursion into 3 types: preorder recursion, postorder recursion and inorder recursion. For now I will write their definitions and describe how they are used in example cases below.
For each of these questions, you want to ask different questions for Main Nodes.
Postorder recursion
The name postorder recursion comes from the tree data structure's postorder recursion like the following:
def postorder(node: Node) -> None:
if node is None: return
postorder(node.left)
postorder(node.right)
print(node.val)
- The actual work, which is the print function in this case, is done after the children nodes are visited.
- If children have to return a result and the parent has to utilize children nodes' returned work, it's a postorder function.
- Most tree related recursive functions have this form.
- Ask these two following questions: "1. What type of work will you the current node have their children do and return? 2. What will you the current node do with your children's work?" for Main Nodes.
Preorder recursion
Similarly, the preorder recursion comes from the preorder function:
def preorder(node: Node) -> None:
if node is None: return
print(node.val)
preorder(node.left)
preorder(node.right)
- The actual work, which is the print function in this case, is done before the children nodes are visited.
- Most of the time, if the recursive function does not require a return value to utilize the collective work from the children nodes, it's a preorder function.
- Ask just one question: "What will you the current node do before visiting children nodes?" for Main Nodes.
- It's also a top down way of thinking about the trees.
- The recursion is pretty much used only for the purpose of iteration. So the function carries around a storage for a result or a global flag.
- Most backtracking solutions have this form.
Inorder recursion
def inorder(node: Node) -> None:
if node is None: return
preroder(node.left)
print(node.val)
preorder(node.right)
- It's similar to preorder in a way except that the real work is done after one of the children nodes is visted.
- Most recursive solutions don't have this form. However, some of my solutions below will have inorder form just for practice.
Path Sum Type Problems
These problems will show you how to think about tree based recursive problems and move our way into backtracking.
Path Sum I (Short-circuiting, Delivering results from child nodes to root)
The following problem is from Leetcode
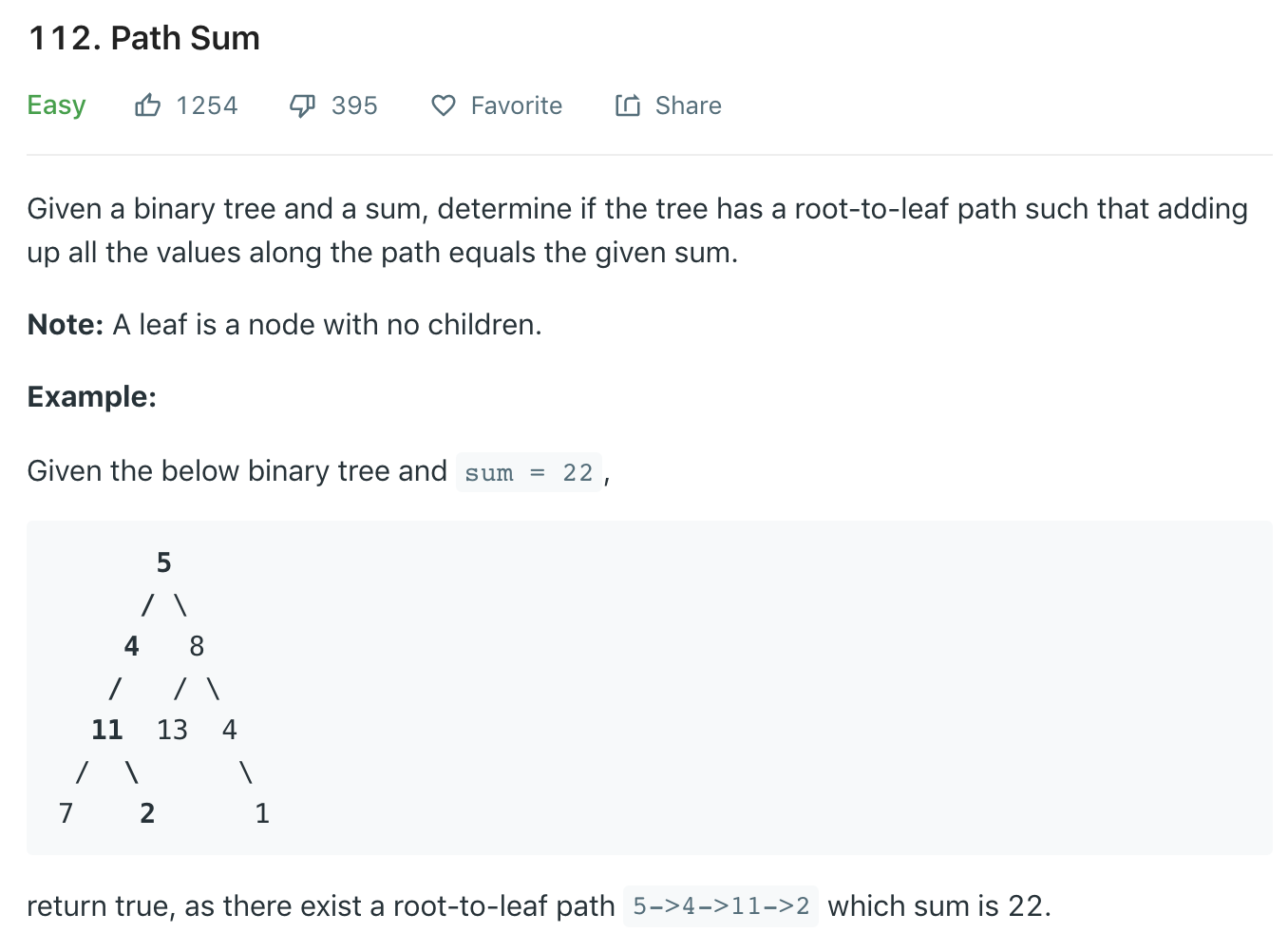
- The decision is made in the leaf node. The base case can include the null node and the leaf node.
Postorder solution
- The parent nodes can pass up the leaf node's decision up to the root node by using the or operator.
- The decision is made from the leaf nodes as a base case. The rest of the non-null nodes carry the decision up to the parent.
- By short-circuiting, its direct children nodes or the subtree below the short-circuiting node is prevented from traversal. However, other parts of the trees can be explored.
- Java
- Python
public boolean postorder(TreeNode node, int inherited) {
if (node == null) return false;
// short-circuiting / base case
if (node.left == null && node.right == null) {
return node.val == inherited;
}
// deliver results made from the base case (leaf nodes and null nodes) to the root node
boolean left = postorder(node.left, inherited - node.val);
boolean right = postorder(node.right, inherited - node.val);
return left || right;
// Another way to write down above code.
// return postorder(node.left, inherited - node.val)
// || postorder(node.right, inherited - node.val);
}
class Solution:
def postorder(self, root: Optional[TreeNode], target: int) -> bool:
if root is None: return False
if root.left is None and root.right is None:
return root.val == target
return self.postorder(root.left, target - root.val) | self.postorder(root.right, target - root.val)
Preorder solution
The result is stored in a global flag.
Base case: If it's a null node, stop the recursion.
In-between node/Root node: If it's a leaf node, change the flag value.
private boolean pathExists;
public void preorder(TreeNode node, int inherited) {
if (node == null) {
return;
}
if (node.left == null && node.right == null) {
if (inherited == node.val) {
pathExists = true;
}
}
preorder(node.left, inherited - node.val);
preorder(node.right, inherited - node.val);
}
Inorder solution
private boolean pathExists;
public void inorder(TreeNode node, int inherited) {
if (node == null) {
return;
}
inorder(node.left, inherited - node.val);
if (node.left == null && node.right == null) {
if (inherited == node.val) {
return pathExists = true;
}
}
inorder(node.right, inherited - node.val);
}
Recursion is used only for iteration. You can call the recursive function anywhere and any number of times and the result will not change.
private boolean pathExists;
public void inorder(TreeNode node, int inherited) {
if (node == null) {
return;
}
inorder(node.right, inherited - node.val);
inorder(node.left, inherited - node.val);
if (node.left == null && node.right == null) {
if (inherited == node.val) {
pathExists = true;
}
}
inorder(node.left, inherited - node.val);
inorder(node.right, inherited - node.val);
}
Path Sum III (Multiple starting root node, how not to short-circuit)
The following problem is from Leetcode

- Trees can have only one root node. Therefore, if the solution or evaluation requires more than one root node as a starting point, you want to have a helper function run on every node to start a new root node.
Helper functions - One root node
- The following functions assume there's only one root node, meaning one start node.
Postorder
- I will start with a wrong solution.
- As the comment says, by returning 1, the function does not search for more paths down the road.
- The postorder code aka the code after the recursive functions does not short-circuit.
private int wrongUtil(TreeNode root, int sum) {
if (root == null) {
return 0;
}
/**
Short-circuiting the finding. If there are multiple ending points it won't find all of them, but
the traversal will be over at the first finding.
*/
if (root.val == sum) {
return 1;
}
return wrongUtil(root.left, sum - root.val) + wrongUtil(root.right, sum - root.val);
}
This does not short-circuit in finding one ending node and continue the search.
private int util(TreeNode root, int sum) {
if (root == null) {
return 0;
}
int leftValue = util(root.left, sum - root.val);
int rightValue = util(root.right, sum - root.val);
int currentNodeValue = root.val == sum ? 1 : 0;
return leftValue + rightValue + currentNodeValue;
}
- The following code does not short-circuit either because it "return" recursive function values, which means it waits until the recursive function goes all the way down.
private int util(TreeNode root, int sum) {
if (root == null) {
return 0;
}
int currentNodeValue = root.val == sum ? 1 : 0;
return currentNodeValue + util(root.left, sum - root.val) + util(root.right, sum - root.val);
}
Preorder
private int counter;
private void util(TreeNode root, int sum) {
if (root == null) {
return;
}
if (root.val == sum) {
counter++;
}
util(root.left, sum - root.val);
util(root.right, sum - root.val);
}
Inorder
private int counter;
private void util(TreeNode root, int sum) {
if (root == null) {
return;
}
util(root.left, sum - root.val);
if (root.val == sum) {
counter++;
}
util(root.right, sum - root.val);
}
Main functions with helper function
- There's only one root node in a tree. We can trigger a util mentioned above in every node.
- Note that the main function is used only for traversal and it does not do any calculation with targetSum because it's used to set a starting point.
Postorder
public int pathSum(TreeNode root, int targetSum) {
if (root == null) return 0;
int left = pathSum(root.left, targetSum);
int right = pathSum(root.right, targetSum);
int current = util(root, targetSum);
return left + right + current;
}
Inorder
public int pathSum(TreeNode root, int targetSum) {
if (root == null) return 0;
pathSum(root.right, targetSum);
util(root, targetSum);
pathSum(root.left, targetSum);
return counter;
}
Inorder traversal with Postorder util
private int counter;
public int pathSum(TreeNode root, int targetSum) {
if (root == null) return 0;
pathSum(root.right, targetSum);
counter += util(root, targetSum);
pathSum(root.left, targetSum);
return counter;
}
- The time complexity of all these solutions is O(N^2) worst case and O(NLogN) best case.
- The space complexity is (N) in worst case and (logN) in best case
Max Path Sum (When to use a global variable)
The following problem is from Leetcode
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root. The path sum of a path is the sum of the node's values in the path. Given the root of a binary tree, return the maximum path sum of any non-empty path.
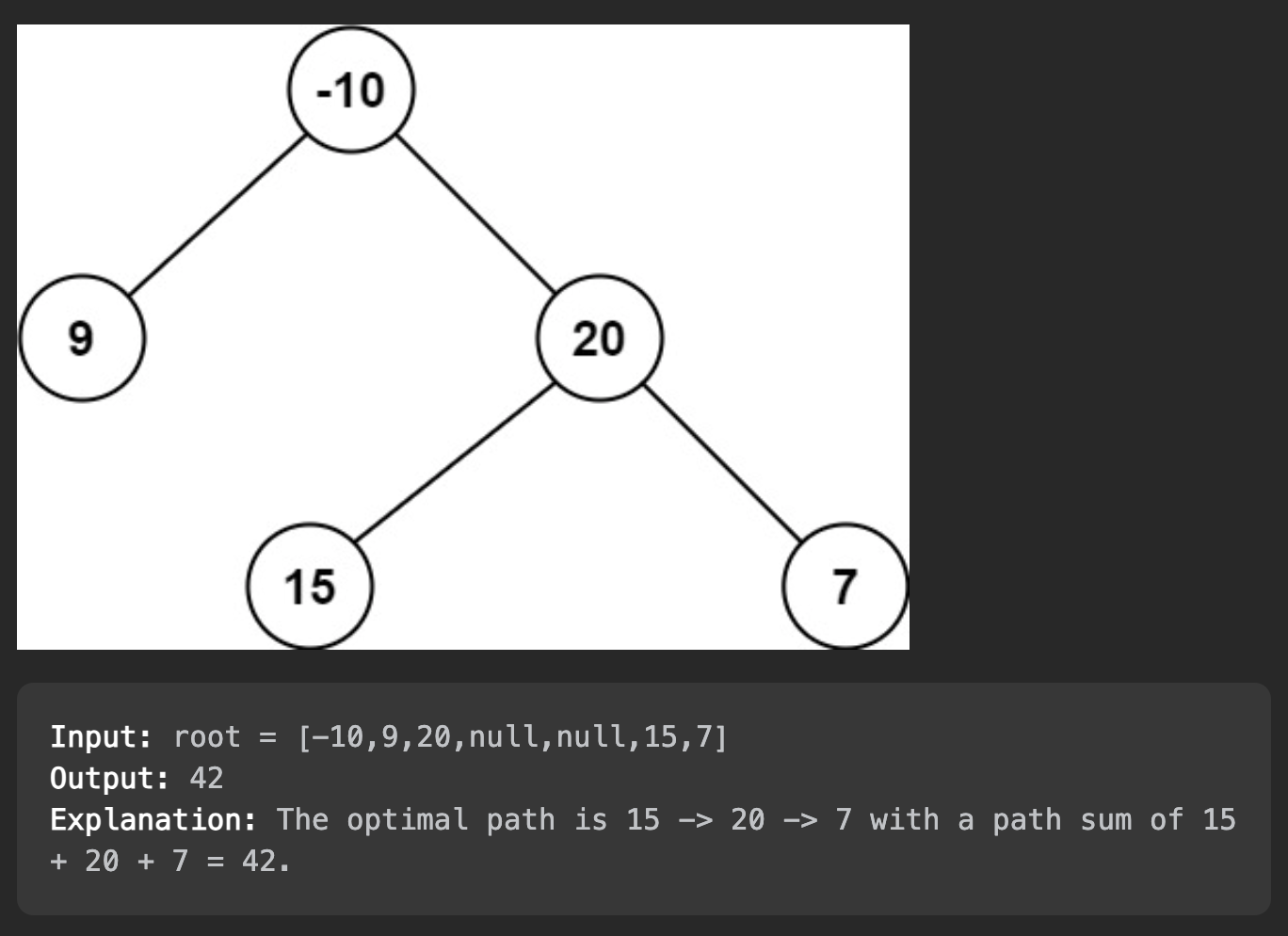
Postorder
- In this problem, we'll only consider postorder.
- The key to this problem is understanding what children nodes can return. At any node, in order to create a path, the ingredients needed are (1) left branch (left child node) (2) right branch (right child node) (3) left branch + right branch + current node (4) the current node. However, in a recursive function, you can't combine left branch and right branch some times and not combine them other times. It's either you combine them on every node or not combine them on every node. Therefore, the evaluation of which is the max value from (1), (2), (3), (4) and the current max can be done locally. And Each node can only return the maximum branch it can find to its parent without combinding the left branch and the right branch. So to return a value, the maximum of (1), (2), (4) is returned.
- How do we not evaluate 0 from the null nodes? (1) Return immediately without evaluating (2) On every level, you're evaluating children + current node or the current node alone. You're never evaluating children nodes alone. With that assumption the children nodes must have evaluated themselves alone.
- Make sure to start from global max value of Integer.MIN_VALUE. If you start with 0, 0 will be evaluated without being part of a tree.
private int pmax = Integer.MIN_VALUE;
private int maxPathSumHelper(TreeNode root) {
if (root == null) return 0;
int left = maxPathSumHelper(root.left);
int right = maxPathSumHelper(root.right);
pmax = Math.max(Math.max(Math.max(Math.max(left + root.val, right + root.val), pmax), root.val), left + right + root.val);
return Math.max(Math.max(left + root.val, right + root.val), root.val);
}
Path Sum II
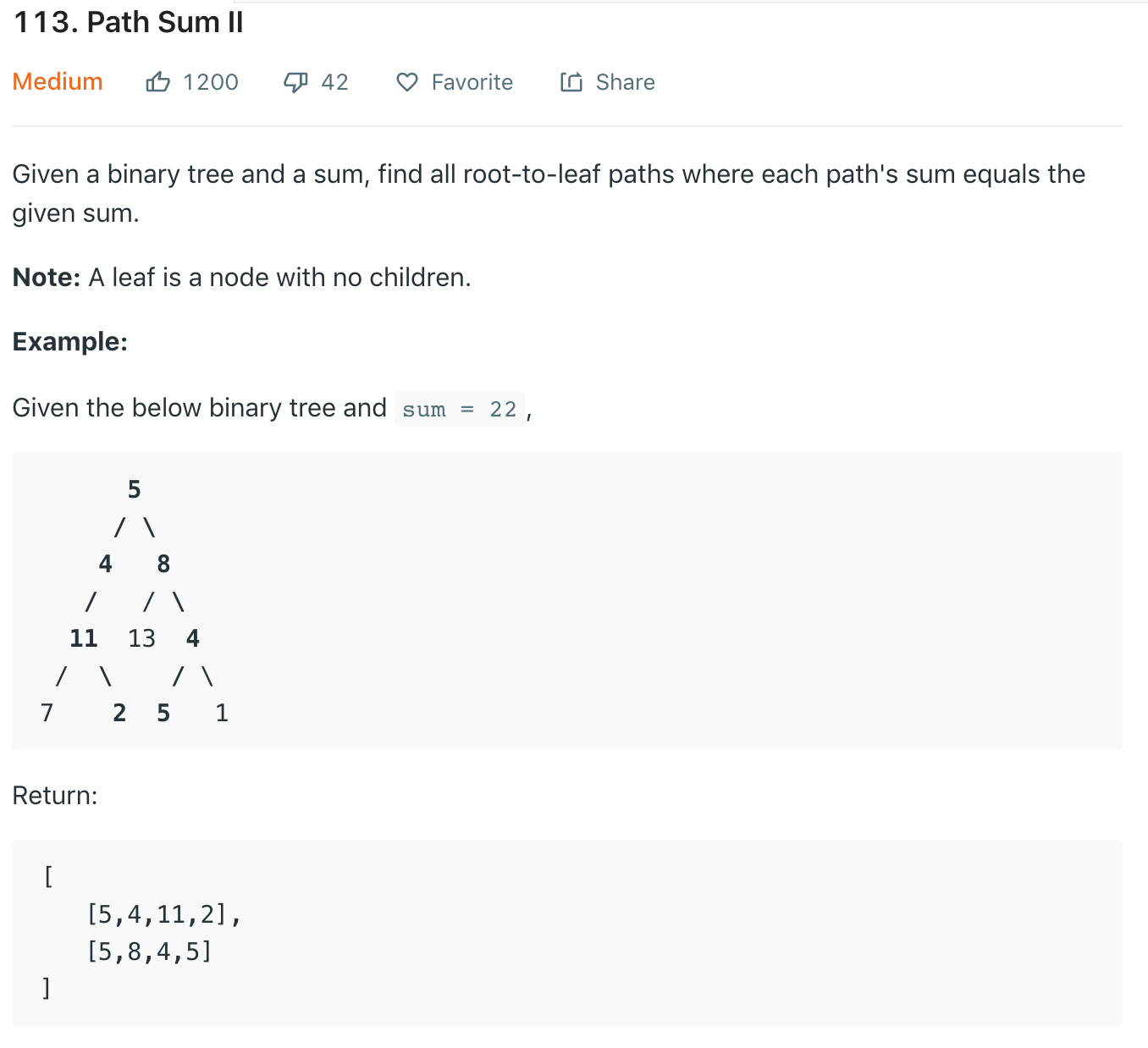
- In this problem, we'll only consider preorder solutions.
Preorder
- intermediateResult to add every element as we go along
- answer to add the intermediateResult in the base case.
- The key to this problem is when to remove a node to keep track of a path from the root to leaf. It's important to recognize that at any level of recursive function, it's always on one path, because it's impossible for two functions to run at the same time and it does not go from one sibling to another sibling. it goes from the parent to the child. It's only after one child is over, the next child is evaluated. For that reason, you just have to focus on removing every node after work at each node is done.
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> answer = new ArrayList<>();
List<Integer> intermediateResult = new ArrayList<>();
preorder(root, targetSum, intermediateResult, answer);
return answer;
}
private void preorder(TreeNode root, int targetSum, List<Integer> intermediateResult, List<List<Integer>> answer) {
if (root == null) {
return;
}
intermediateResult.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
answer.add(new ArrayList<>(intermediateResult));
}
}
preorder(root.left, targetSum - root.val, intermediateResult, answer);
preorder(root.right, targetSum - root.val, intermediateResult, answer);
/**
leaf nodes and non leaf nodes can reach this line,
because there's no short-circuiting in the leaf nodes.
*/
intermediateResult.remove(intermediateResult.size() - 1);
}
- It's very important to visualize this line of code
intermediateResult.remove(intermediateResult.size() - 1);. if you are a leaf node, both of your left and right null nodes are visited and they are not added to the intermediate result and the decision of whether to add to the result or not is made up there, and now you just need to remove yourself because the recursive calls are at the end. There's no more results to verify. If you are a non-leaf node, your left and right children are just traversed and you need to remove yourself before the function is over, so your parent can now traverse the next child of candidate. Note that removal is done in the post order level, which means all the work is already done and you want to prepare for the next work and the only preparation you need to do is removing yourself, so the next nodes can be added. - Would the following code work?
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> answer = new ArrayList<>();
List<Integer> intermediateResult = new ArrayList<>();
preorder(root, targetSum, intermediateResult, answer);
return answer;
}
private void preorder(TreeNode root, int targetSum, List<Integer> intermediateResult, List<List<Integer>> answer) {
if (root == null) {
return;
}
intermediateResult.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
answer.add(new ArrayList<>(intermediateResult));
}
return; // will this work?
}
preorder(root.left, targetSum - root.val, intermediateResult, answer);
preorder(root.right, targetSum - root.val, intermediateResult, answer);
intermediateResult.remove(intermediateResult.size() - 1);
}
No, it would not work, because the leaf nodes cannot remove themselves. But the leaf nodes have to wait until its parent to visit both leaf nodes until the parent removes only one of its leaf child. Leaf nodes can't go all the way down to the preorder recursive calls to call its null left and null right and then remove itself from the list in the last line of code. It seems like it could work because it seems like the parent node is removing the child node in the list. But the caveat is that the parent node can remove only the right leaf node if there are both left and right leaf nodes.
Then if I keep the return statement in the leaf node if statement and add removing the leaf node part, would the following code work?
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> answer = new ArrayList<>();
List<Integer> intermediateResult = new ArrayList<>();
preorder(root, targetSum, intermediateResult, answer);
return answer;
}
private void preorder(TreeNode root, int targetSum, List<Integer> intermediateResult, List<List<Integer>> answer) {
if (root == null) {
return;
}
intermediateResult.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
answer.add(new ArrayList<>(intermediateResult));
}
intermediateResult.remove(intermediateResult.size() - 1); // newly added code
return;
}
preorder(root.left, targetSum - root.val, intermediateResult, answer);
preorder(root.right, targetSum - root.val, intermediateResult, answer);
intermediateResult.remove(intermediateResult.size() - 1);
}
Yes, it does. (TODO: add some visualization as to why it works) Why? Because now the leaf nodes get to remove themselves and the parent nodes, after visiting its left and right children, get to remove themselves from the list. So every node of the tree gets to remove themselves. If a node has two leaf children, the children will be removed in the if block. If a node has one null and one child, the null part was never added to the list and non null child was removed. So after its children are removed, the node just has to remove itself.
Important to note that if you don't have the return statement and only remove in the leaf node if statement, it will not work either. The reason is now the leaf nodes will visit its left null and right null with the recursive calls in the next lines of code and will try to remove itself again in the last line of code.
Another way to remove nodes and continue the list is the following. By checking if a node is null before traversing, you don't have to add the if (root == null) check.
private void preorder(TreeNode root, int targetSum, List<Integer> intermediateResult, List<List<Integer>> ans) {
intermediateResult.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
ans.add(new ArrayList<>(intermediateResult));
}
intermediateResult.remove(intermediateResult.size() - 1);
return;
}
if (root.left != null) {
preorder(root.left, targetSum - root.val, intermediateResult, ans);
}
if (root.right != null) {
preorder(root.right, targetSum - root.val, intermediateResult, ans);
}
intermediateResult.remove(intermediateResult.size() - 1);
}
Would this work?
private void preorder(TreeNode root, int targetSum, List<Integer> intermediateResult, List<List<Integer>> ans) {
intermediateResult.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
ans.add(new ArrayList<>(intermediateResult));
}
}
if (root.left != null) {
preorder(root.left, targetSum - root.val, intermediateResult, ans);
}
if (root.right != null) {
preorder(root.right, targetSum - root.val, intermediateResult, ans);
}
intermediateResult.remove(intermediateResult.size() - 1); // leaf nodes remove itself here too
}
Yes, it does.
Now consider the following variation. Would this work?
private void preorder(TreeNode root, int targetSum, List<Integer> intermediateResult, List<List<Integer>> ans) {
intermediateResult.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
ans.add(new ArrayList<>(intermediateResult));
}
return;
}
if (root.left != null) {
preorder(root.left, targetSum - root.val, intermediateResult, ans);
// only done by the parent, leaf nodes never get here.
intermediateResult.remove(intermediateResult.size() - 1);
}
if (root.right != null) {
preorder(root.right, targetSum - root.val, intermediateResult, ans);
// only done by the parent, leaf nodes never get here.
intermediateResult.remove(intermediateResult.size() - 1);
}
}
Yes, because the parent removes its left child and right child. Every node is visiting the left child node only if it exists and remove that element only if it was added in the first place; same goes for the right child node. Note that the node is not removing itself but the parent is removing its child node, so the root node can never be removed. The remove statement is only after checking if the child nodes exist or not. So the root node never gets to remove itself. However, it works, because the root node never has to be removed since it's finding the path from root to leaf.
The difference between this code and the above code in which the parent node removes its child node is that both left and right child gets removed by the parent but the earlier one can have only right node be removed if there are both left and right leaf nodes.
Now consider the following variation.
Would this work?
private void preorder(TreeNode root, int targetSum, List<Integer> intermediateResult, List<List<Integer>> answer) {
if (root == null) {
return;
}
intermediateResult.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
answer.add(new ArrayList<>(intermediateResult));
}
}
preorder(root.left, targetSum - root.val, intermediateResult, answer);
intermediateResult.remove(intermediateResult.size() - 1);
preorder(root.right, targetSum - root.val, intermediateResult, answer);
intermediateResult.remove(intermediateResult.size() - 1);
}
No because the key is going all the way down to the null node.
Backtracking
Subsets
Now you will see why recursive way of thinking is important. It's because you can turn turn some problems into trees and recursion provides an exhaustive solution.
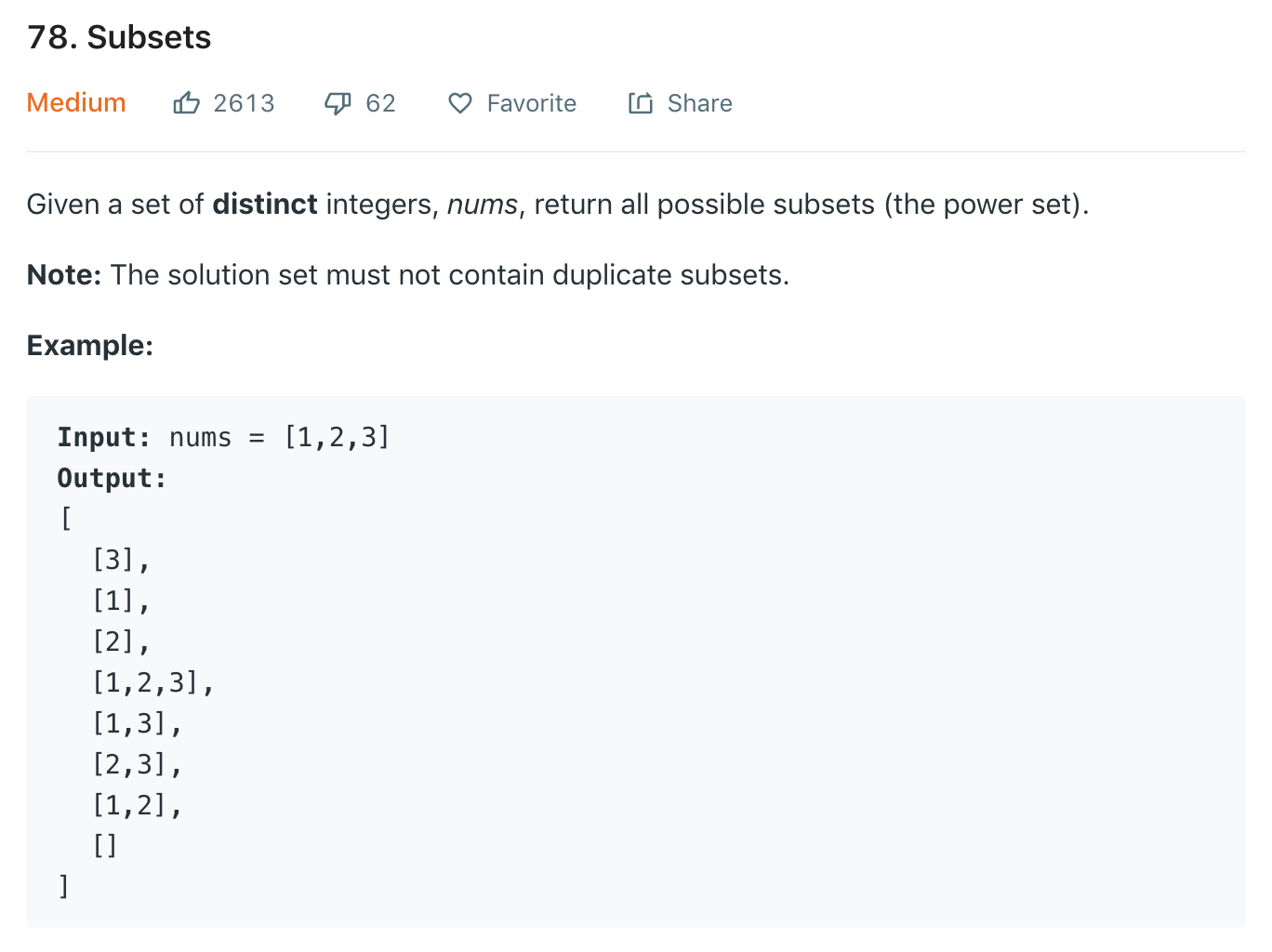
You can turn this problem into the form of trees by think of it as n-ary tree nodes.
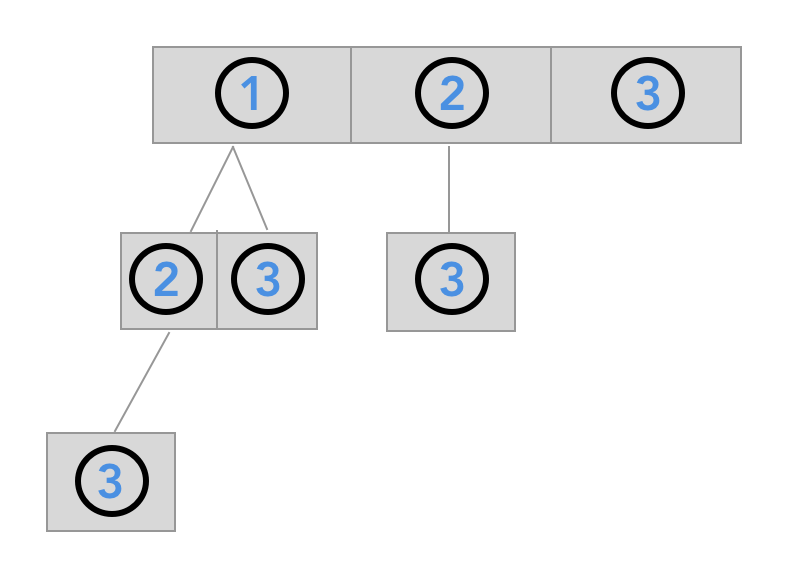
Every node is generating a subset. In the first node 1 is generating [1] and its child 2 is generating [1,2]. Then 2's child 3 generates [1,2,3]. You can solve this problem like pathsum 2 except that you are adding every list from the root to a child node to the final result.
- Time complexity: [Question for Yanqing]
- Space complexity: [Question for Yanqing]
public List<List<Integer>> subsets(int[] nums) {
List<Integer> intermediateResult = new ArrayList<>();
List<List<Integer>> answer = new ArrayList<>();
preorder(nums, 0, intermediateResult, answer);
return answer;
}
private void preorder(int[] nums, int start, List<Integer> intermediateResult, List<List<Integer>> answer ) {
answer.add(new ArrayList<>(intermediateResult));
for (int i = start; i < nums.length; i++) { // 1
int cur = nums[i];
intermediateResult.add(cur);
preorder(nums, i + 1, intermediateResult, answer);
// after going through one child, each node is removing itself before moving onto its sibling.
intermediateResult.remove(intermediateResult.size() - 1);
}
}
It's important to understand when intermediate result list is added to the answer list and when the node is removed from the list. the answer starts in beginning of the function by adding the empty intermediate result. For every node it adds to the intermediate result and the intermdiate result is added to the answer list in its child node level. And the node is removed from the intermeidate list after every level of chis is explored and before moving onto its sibling.
Postorder
private List<List<Integer>> postorder(int[] nums, int level) {
if (level == nums.length) {
List<Integer> il = new ArrayList<>();
List<List<Integer>> list = new ArrayList<>();
list.add(il);
return list;
}
List<List<Integer>> childrenResult = postorder(nums, level + 1);
List<List<Integer>> newResult = new ArrayList<>();
int currentNode = nums[level];
for (int i = 0; i < childrenResult.size(); i++) {
List<Integer> childResult = childrenResult.get(i);
newResult.add(new ArrayList<>(childResult));
newResult.add(childResult);
childResult.add(currentNode);
}
return newResult;
}