HashMap and Sliding Windows
2Sum Related Problems
Solutions python
- https://leetcode.com/problems/two-sum/
- https://leetcode.com/problems/two-sum-ii-input-array-is-sorted/
- https://leetcode.com/problems/3sum/
- Leetcode - 560. Subarray Sum Equals K
Bruteforce N^3
- Time complexity: N^3
- Space: O(1)
public int subarraySum(int[] nums, int k) {
int counter = 0; //
for (int start = 0; start < nums.length; start++) {//
for (int end = start; end < nums.length; end++) { //
int sum = 0;
for (int i = start; i <= end; i++) {
sum += nums[i];
}
if (sum == k) { //
counter++;
}
}
}
return counter;
}
Bruteforce N^2
- Time complexity: N^2
- Space: O(1)
public int subarraySum(int[] nums, int k) {
int counter = 0; // 1
for (int start = 0; start < nums.length; start++) {//2
int sum = nums[start]; //3
for (int end = start; end < nums.length; end++) { //2
if (start != end) {
sum += nums[end]; //
}
if (sum == k) { // 3 == 3?
counter++;
}
}
}
return counter;
}
O(N) solution
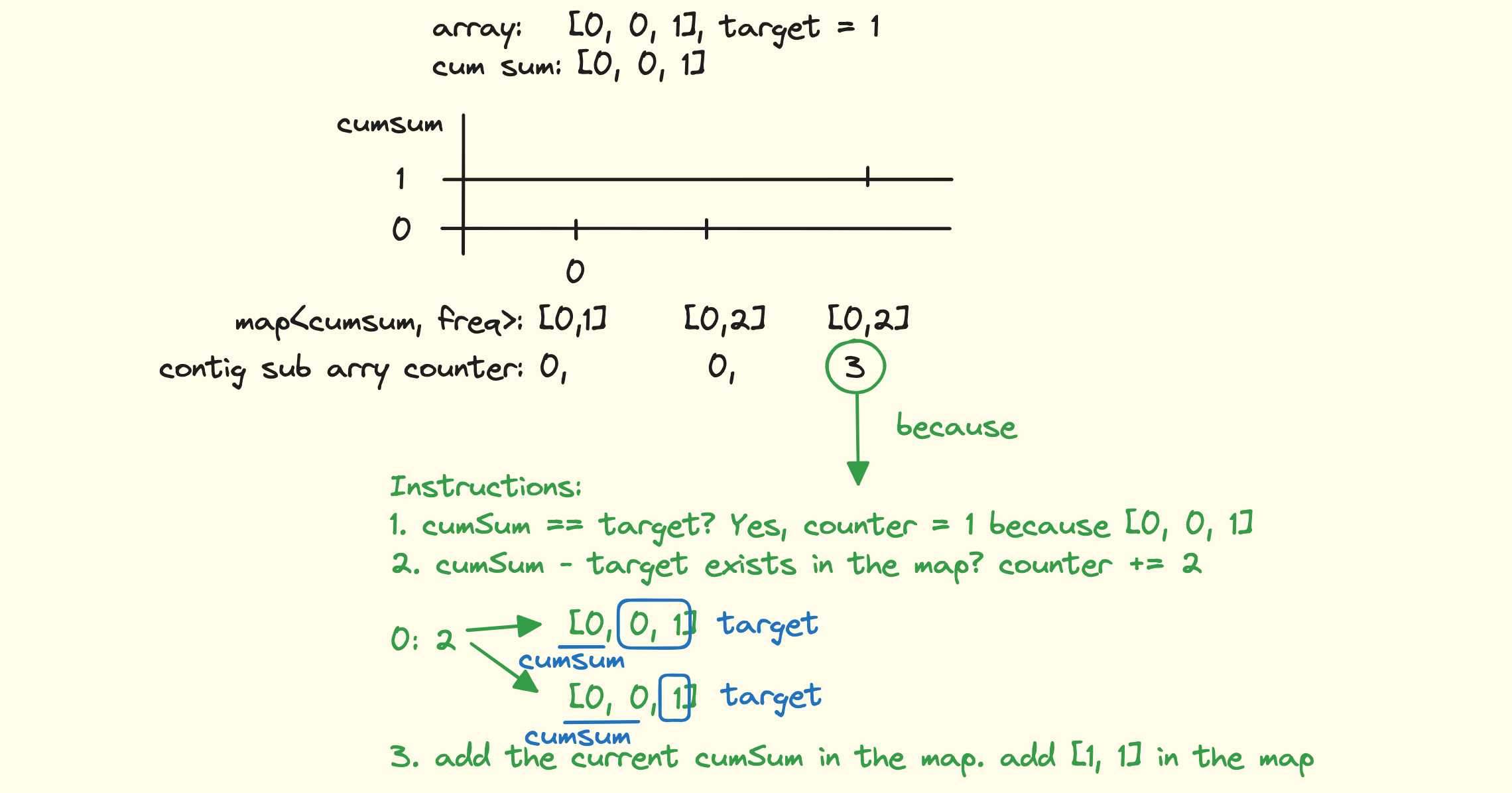
- Keep track of cumulative sum in every index. At every index subtract k from cumulative sum up to that point. If the subtracted value exists in the map, it means there is a contiguous subinterval that ends at the current index and sums to k, because there was a contiguous subinterval in the previous iteration up to the subinterval that ends at the current index and sums to k.
- Time complexity: O(N)
- Space complexity: O(N)
public int subarraySum(int[] nums, int target) { // 1
int counter = 0;
Map<Integer, Integer> sumMap = new HashMap<>();
int cumSum = 0; // 0
for (int i = 0; i < nums.length; i++) {
cumSum += nums[i]; // 0 + 1 = 1
if (cumSum == target) counter++;
int remnant = cumSum - target; // 1 - 1 = 0
if (sumMap.containsKey(remnant)) {
counter += sumMap.get(remnant); // 1 + 2 = 3
}
sumMap.put(cumSum, sumMap.getOrDefault(cumSum, 0) + 1);
}
return counter;
}
Sliding windows
Minimum window substring
- https://leetcode.com/problems/minimum-window-substring/description/ This is a good problem to start with because the solution to this problem can be used for the rest of the problems on the list.
In this algorithm, which solves the minimum window substring problem, there are two pointers: right and left.
Here, the word requirements is used to refer to the characters in the string p that needs to be contained in the window to return as an answer.
- Right pointer: satisfies the requirements, which means as it goes through the string s, it tries to collect all the required characters from the string p.
- Left pointer: it breaks the requirement satisfaction but only at most one character will be missing
Note that as soon as the right pointer is done satisfying the requirements, at most only one requirement is broken broken by the left pointer. After that the right pointer moves on to satisfy the broken requirement and might collect already satisfied required characters.
The hashmap associates to each character T an integer value N, which can be positive, negative, or zero.
- Positive value: the right pointer still needs to see N copies of the character T.
- Zero: the required number of copies for the character T was seen.
- Negative value: the right pointer has seen more than the required copies of the character T.
Error counter is an integer value E, which can be positive or zero.
Positive value: the right pointer still needs to see E different characters.
Zero: the right pointer has seen E types of chracter, which meets the requirement.
Time complexity: O([length of string s = M] + [length of string t = N]). Precisely: 2M + N
Space complexity: O(length of string t)
public String minWindow(String s, String t) {
if (t.length() > s.length()) {
return "";
}
int left = 0;
Map<Character, Integer> tmap = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
Character c = t.charAt(i);
tmap.put(c, tmap.getOrDefault(c, 0) + 1);
}
int error = tmap.size();
int minsize = s.length();
String substring = "";
for (int right = 0; right < s.length(); right++) {
Character c = s.charAt(right);
if (tmap.containsKey(c)) {
tmap.put(c, tmap.get(c) - 1);
if (tmap.get(c) == 0) {
error--;
}
}
while (error == 0) {
int cursize = right - left + 1;
if (cursize <= minsize) {
minsize = cursize;
substring = s.substring(left, right + 1);
}
Character lc = s.charAt(left);
if (tmap.containsKey(lc)) {
tmap.put(lc, tmap.get(lc) + 1);
if (tmap.get(lc) > 0) {
error++;
}
}
left++;
}
}
return substring;
}
The following code uses Pair to add only the characters that belong to T.
public String minWindow(String s, String t) {
// character, count
Map<Character, Integer> map = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
char cur = t.charAt(i);
map.put(cur, map.getOrDefault(cur, 0) + 1);
}
List<Pair<Character, Integer>> filtered = new ArrayList<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (map.containsKey(c)) {
filtered.add(new Pair<Character, Integer>(c, i));
}
}
int minLen = s.length();
String minString = "";
int error = map.size();
int left = 0;
for (int i = 0; i < filtered.size(); i++) {
Pair curPair = filtered.get(i); //(a,3)
char cur = (char) curPair.getKey(); // a
int curI = (int) curPair.getValue();//3
map.put(cur, map.get(cur) - 1);
if (map.get(cur) == 0) error--;
while (error == 0) {
int leftI = filtered.get(left).getValue(); // 2
int curLen = curI - leftI + 1; // 3 - 2 + 1
if (curLen <= minLen) {
minLen = curLen;
minString = s.substring(leftI, curI + 1);
}
char leftChar = filtered.get(left).getKey(); // a
map.put(leftChar, map.get(leftChar) + 1);
if (map.get(leftChar) == 1) {
error++;
}
left++;
}
}
return minString;
}
All anagrams
This problem can also be solved with the same solution as the minimum window problem. The difference is what requirement the substring has to satisfy. In order to check if the right pointer has gathered only the strings from p in s, the error count needs to be 0 and the length of the string in the window needs to be same as that of p.
- Time complexity: O([length of string s = M] + [length of string t = N]). Precisely: 2M + N
- Space complexity: O(26) = O(1) because the map will have distinct characters, which is O(26)
public List<Integer> findAnagrams(String s, String p) {
List<Integer> answer = new ArrayList<>();
if (p.length() > s.length()) {
return answer;
}
Map<Character, Integer> pmap = new HashMap<>();
for (int i = 0; i < p.length(); i++) {
Character c = p.charAt(i);
pmap.put(c, pmap.getOrDefault(c, 0) + 1);
}
int error = pmap.size();
int left = 0;
for (int right = 0; right < s.length(); right++) {
Character rc = s.charAt(right); // b
if (pmap.containsKey(rc)) {
pmap.put(rc, pmap.get(rc) - 1);
if (pmap.get(rc) == 0) {
error--;
}
}
while (error == 0) {
if (right - left + 1 == p.length()) {
answer.add(left);
}
Character lc = s.charAt(left);
if (pmap.containsKey(lc)) {
pmap.put(lc, pmap.get(lc) + 1);
if (pmap.get(lc) > 0) {
error++;
}
}
left++;
}
}
return answer;
}
At most two distinct characters
This one is again similar to minimum window. The difference in the algorithm is that
the right pointer: it goes as far as it can while meeting the requirements and it will stop when it breaks meeting the requirement in the beginning. Then after the left pointer moves to meet the requirement, the right pointer starts breaking the requirement.
the left pointer: it is used to meet the requirement when the right pointer broke just broke the requirements.
The maximum length comparison check is done in the following cases:
- When the right pointer is in the process of meeting the requirement during its first iterations.
- When the right pointer is stretching its limit and keeps iterating until it breaks the requirement, which means the current length of the window is at least size 2.
It's important to notice that the maximum length comparison is not done all the time when the requirements are met. When the right pointer breaks the requirement by one character so the left pointer had to do the job of meeting the requirements, which is one for loop iteration, there's no maximum length comparison during this iteration. It means after meeting the maximum length of 2, which is done by the first for loop iteration by by the right pointer, the same length is not recorded in the following iterations. However, this is fine, because when the requirement was first met the minimum length was recorded.
public int lengthOfLongestSubstringTwoDistinct(String s) {
if (s.length() == 1) {
return 1;
}
Map<Character, Integer> map = new HashMap<>();
int maxlength = 0;
int left = 0;
for (int right = 0; right < s.length(); right++) {
Character rc = s.charAt(right);
map.put(rc, map.getOrDefault(rc, 0) + 1); // breaks the requirement
if (map.size() <= 2) { // this gets called only when it first met the requirement: length 2 or the length is greater than 2
int curlength = right - left + 1;
if (maxlength < curlength) {
maxlength = curlength;
}
}
while (map.size() > 2) { // meeting the requirements
Character lc = s.charAt(left);
map.put(lc, map.get(lc) - 1);
if (map.get(lc) == 0) {
map.remove(lc);
}
left++;
}
}
return maxlength;
}
At most k distinct characters
The solution is very similar to the solution above about the 2 distinct characters. You just have to replace 2 with k.
Time complexity: O(N = length of s) Space complexity: O(N = length of s)
public int lengthOfLongestSubstringKDistinct(String s, int k) {
if (k == 0) return 0;
if (s.length() == 1) {
return 1;
}
Map<Character, Integer> map = new HashMap<>();
int minlength = 0;
int left = 0;
for (int right = 0; right < s.length(); right++) {
Character rc = s.charAt(right); // e
map.put(rc, map.getOrDefault(rc, 0) + 1);
if (map.size() <= k) {
int curlength = right - left + 1;
if (minlength < curlength) {
minlength = curlength;
}
}
while (map.size() > k) {
Character lc = s.charAt(left);
map.put(lc, map.get(lc) - 1);
if (map.get(lc) == 0) {
map.remove(lc);
}
left++;
}
}
return minlength;
}
Subarrays with K different Integers
The important part about this algorithm is that the cardinality of exactly K is equal to [the cardinality of at most K] - [the cardinality of at most K - 1].
Another thing about the solution is that the subarray count is same as the length of the array.
Suppose with an initial window [a], subarrays that ends with this element are [a]--> 1 Then the window is exapnaded to [a,b]. The subarrays that ends with this new element are [b], [a,b] -->2 Now the window expanded to [a,b,c]. Subarrays that ends with this new element are [c], [b, c], [a,b,c] -->3
For this reason in my solution, I do subarray count += window length.
Time complexity: O(N = nums.length) Space complexity: O(k)
public int subarraysWithKDistinct(int[] nums, int k) {
return atMostK(nums, k) - atMostK(nums, k-1);
}
public int atMostK(int[] nums, int k) {
int left = 0, count = 0;
Map<Integer, Integer> map = new HashMap<>();
for (int right = 0; right < nums.length; right++) {
int rnum = nums[right]; //1
map.put(rnum, map.getOrDefault(rnum, 0) + 1);
while (map.size() > k && left < nums.length) {
int lnum = nums[left];
map.put(lnum, map.get(lnum) - 1);
if (map.get(lnum) == 0) {
map.remove(lnum);
}
left++;
}
count += right - left + 1; // 1
}
return count;
}
Concatenation
https://leetcode.com/problems/substring-with-concatenation-of-all-words/description/
Time complexity: O(N a b) where N is the length of string s and a is the length of words and b is the length of each word.
Space complexity: O(a + b)
Question: In the second for loop, why does
left + bigwindowfaster thanslength - smwindow?For space complexity, would O(a b) make sense? O(a b) would be the character size of the words and technically that many characters will be stored.
public List<Integer> findSubstring(String s, String[] words) {
int smwindow = words[0].length();
int bigwindow = words.length * smwindow;
List<Integer> answer = new ArrayList<>();
if (s.length() < bigwindow) {
return answer;
}
Map<String, Integer> wordmap = new HashMap<>();
for (int i = 0; i < words.length; i++) {
wordmap.put(words[i], wordmap.getOrDefault(words[i], 0) + 1);
}
int slength = s.length();
for (int left = 0; left <= slength - bigwindow; left++) {
Map<String, Integer> interm = new HashMap<>();
// the following for exceeds time limit.
for (int right = left; right <= slength - smwindow; right += smwindow) {
// in order to pass, this for loop works:
// for (int right = left; right < left + bigwindow; right += smwindow)
//System.out.println(left + ", " + right);
String substring = s.substring(right, right + smwindow);
if (wordmap.containsKey(substring)) {
interm.put(substring, interm.getOrDefault(substring, 0) + 1);
if (interm.equals(wordmap)) {
answer.add(left);
break;
}
} else {
break;
}
}
}
return answer;
}