Search

Algorithms

1. Binary Search (iterative and recursive)

• Getting mid is (left + right) / 2 because median is a special case of average.

Iterative

• Make sure the items are sorted already
• Time complexity: O(Log N)

public int binarySearch(int[] nums, int target) {
    int left = 0; right = nums.length - 1;
    while (left <= right) {
        int mid = (right + left) / 2;
        if (nums[mid] < target) {
            right = mid - 1;
        } else if (nums[mid] > target) {
            left = mid + 1;
        } else {
            return mid;
        }
    }
    return -1;
}

Recursive

public int binarySearch(int[] nums, int target, int left, int right) {
    if (left > right) return -1;

    int mid = (right + left) / 2;
    if (nums[mid] < target) {
        right = mid - 1;
        return binarySearch(nums, target, left, right);
    } else if (nums[mid] > target) {
        left = mid + 1;
        return binarySearch(nums, target, left, right);
    } else {
        return mid;
    }
}

Converge

• No short-circuiting
• The element has to exist in the array
• when the element equals target, right = mid instead of left = mid to prevent infinite loop.

public int binarySearch(int[] nums, int target) {
    int left = 0; right = nums.length - 1;    
     while (left < right) {
        int mid = (right + left) / 2;
        if (target < nums[mid]) {
            right = mid - 1;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid;
        }
     }
     return left;
}

2. Nearest neighbor binary search

public int binarySearch(int[] nums, int target) {
    int left = 0; right = nums.length - 1;
    int nearest = -1;
    while (left <= right) {
        if (left == right) return left;
        int mid = (right + left) / 2;
        if (nums[mid] < target) {
            right = mid - 1;
        } else if (nums[mid] > target) {
            left = mid + 1;
        } else {
            return mid;
        }
    }
    
    if (left < nums.length && nums[left] - target > target - nums[right]) {
        nearest = left;
    } else if (right >= 0 && target - nums[right] < nums[left] - target) {
        nearest = right;
    } else if (left == nums.length) {
        nearest = nums.length - 1;
    } else if (right < 0) {
        nearest = 0;
    }
    
    return nearest;
}

• If the target number does not exist in the array, it's assumed that the last element evaluated, meaning the item where left == right, is one of the closest element.

• When the loop is over, left > right.

• If left or right is out of bounds, the index 0 or nums.length - 1 needs to be returned, because it means the target number is less than the least number or the target number is greater than the greatest element.

Practice Problems

0. Leetcode - First Bad Version

• Converge binary search
• int mid = left + (right - left) / 2; to prevent integer overflow.

public int firstBadVersion(int n) {
    int left = 0, right = n;
    while (left < right) {
      int mid = left + (right - left) / 2;
      if (isBadVersion(mid)) {
        right = mid;
      } else { // good version
        left = mid + 1;
      }
    }
    return left;
}

1. https://leetcode.com/problems/find-k-closest-elements

• Time Complexity: O(N)
• Space Complexity: O(1)

public List<Integer> findClosestElements(int[] arr, int k, int target) {
    if (k >= arr.length) {
        return Arrays.stream(arr).boxed().collect(Collectors.toList());
    }
    int left = 0;
    int right = arr.length - 1;
    while (right - left + 1 != k) {
        int mid = (right + left) / 2;
        if (target - arr[left] > arr[right] - target) {
            left++;
        } else {
            right--;
        }
    }
    List<Integer> ans = new ArrayList<>();
    while (left <= right) {
        ans.add(arr[left]);
        left++;
    }
    return ans;
}

• The purpose is to find the best window, so you need to compare the left and right not the mid, meaning the if statement needs to be like this if (target - arr[left] > arr[right] - target) {

2. https://leetcode.com/problems/search-a-2d-matrix/

• Time complexity: O(N) the size of matrix

• Space complexity: O(1)

• The key of this algorithm is to convert the mid value into row and column and continue the search as if it's a long array

[0, 1, 2, 3, 4, 5, 6, 7]
[8, 9, 10, 11, 12, 13, 14]
public boolean searchMatrix(int[][] matrix, int target) {
    int left = 0;
    int rowCount = matrix.length;
    int colCount = matrix[0].length;
    int right = rowCount * colCount - 1;
    
    while (left <= right) {
        int mid = (left + right) / 2;
        // translate
        int row = mid / colCount; // 11/7 = 1
        int col = mid % colCount;
        
        if (matrix[row][col] < target) {
            left = mid + 1;
        } else if (matrix[row][col] > target) {
            right = mid - 1;
        } else {
            return true;
        }
    }
    
    return false;
}

3. https://leetcode.com/problems/search-in-rotated-sorted-array/

• Time Complexity: O(log N)

• Space Complexity: O(1)

• The key is you have to check for the rotation area first. If the left is sorted, then see if the target belongs to the left.

public int search(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) return mid;
        
        if (nums[mid] < nums[right]) { // check for the rotation first
            // mid to right is sorted
            if (nums[mid] < target && target <= nums[right]) { // mid < target <= right
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        } else { // if (nums[left] < nums[mid])
            // left to mid is sorted
            if (nums[mid] > target && target >= nums[left]) { // left <= target < mid
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
    }
    return -1;
}

4. https://leetcode.com/problems/median-of-two-sorted-arrays/

5. Leetcode - Leftmost Column with at Least a One

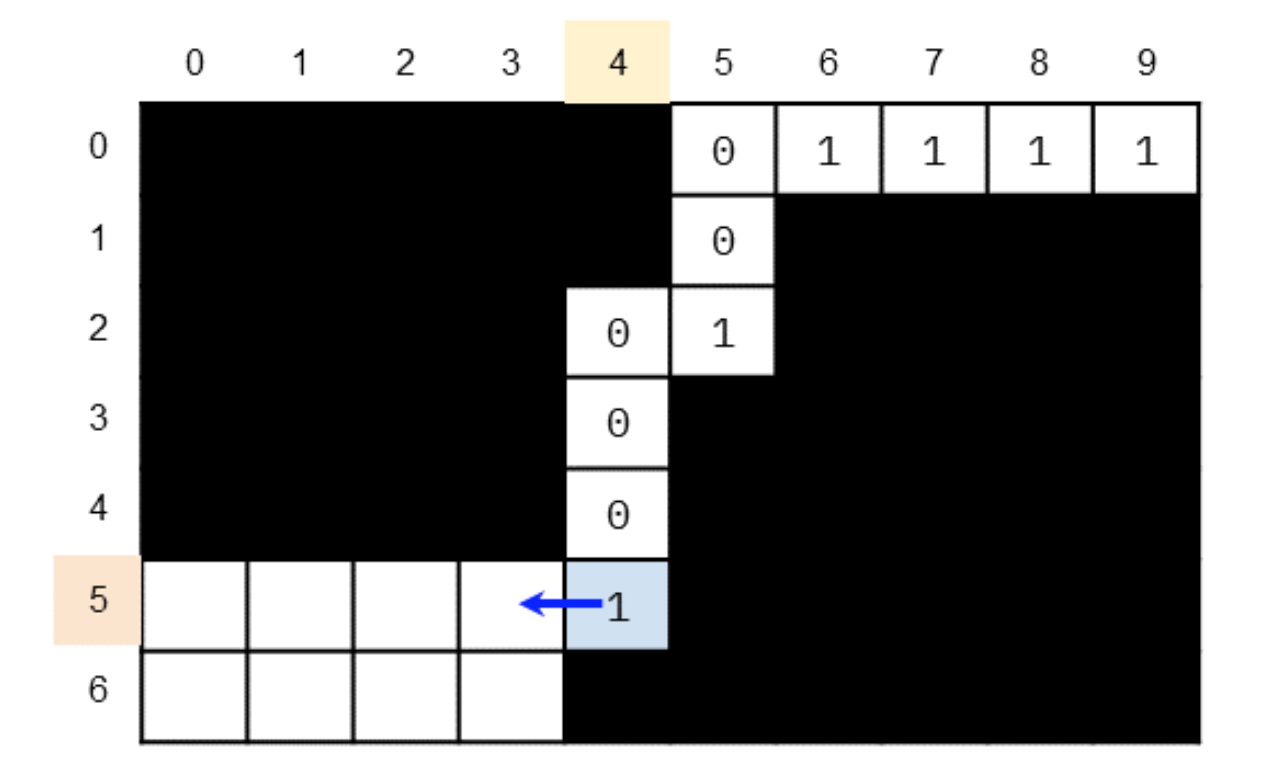
public int leftMostColumnWithOne(BinaryMatrix bm) {
    this.minCol = Integer.MAX_VALUE;
    this.rowSize = bm.dimensions().get(0);
    this.colSize = bm.dimensions().get(1);
    traverse(bm, 0, colSize - 1);
    if (minCol == Integer.MAX_VALUE) return -1;
    return minCol;
}
private int minCol, rowSize, colSize;
private void traverse(BinaryMatrix bm, int row, int col) {
    if (row < 0 || row == this.rowSize || col < 0 || col == this.colSize) return;

    int cur = bm.get(row, col);
    if (cur == 1) { // move left
        minCol = Math.min(minCol, col);
        traverse(bm, row, col - 1);
    } else { // move down
        traverse(bm, row + 1, col);
    }
}